Question

The distance of a point $\left( {1, - 5,9} \right)$ from the plane $x - y + z = 5$ measured along the line $x = y = z$ is
A) $3\sqrt {10} $
B) $10\sqrt 3 $
C) $\dfrac{{10}}{{\sqrt 3 }}$
D) $\dfrac{{20}}{3}$

Answer 1

Hint:Here we can write the equation of the line as point is given $\left( {1, - 5,9} \right)$. And direction ratio is also given as $\left( {1,1,1} \right)$. So equation is written by
$\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = \dfrac{{z - {z_1}}}{c}$ where $\left( {x,y,z} \right)$ are the points and $\left( {a,b,c} \right)$ are the direction ratios.Using this equation we find the coordinate points on the plane then finally we calculate distance between these two points which is our required answer.

Complete step-by-step answer:
Here, a plane is given $x - y + z = 5$ and a point anywhere is given $\left( {1, - 5,9} \right)$ which is to be measured along the line $x = y = z$. So if we draw the diagram, it seems like this:

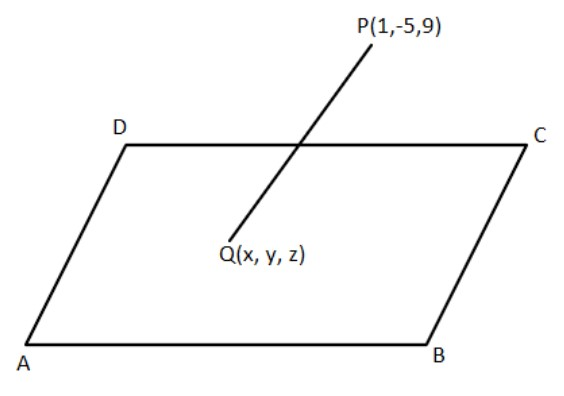
So here, $ABCD$ is a plane satisfying $x - y + z = 5$ and $Q$ is the point on this plane and $P$ is the given point and $PQ$ is the line along $x = y = z$.
So we need to find $PQ$.
So for that we need to find the coordinates of $Q$.
Here the point $P\left( {{x_1},{y_1},{z_1}} \right) = \left( {1, - 5,9} \right)$ is given. And the point $Q\left( {x,y,z} \right)$ is assumed.
And we are given that $PQ$ is along the line $x = y = z$, that means we are given a direction ratio, that is $\left( {1,1,1} \right)$.
So equation of line $PQ$ must be written as
$\dfrac{{x - {x_1}}}{{{{\left( {dr} \right)}_1}}} = \dfrac{{y - {y_1}}}{{{{\left( {dr} \right)}_2}}} = \dfrac{{z - {z_1}}}{{{{\left( {dr} \right)}_3}}}$
Here $dr$ is the direction ratio.
So, $\dfrac{{x - 1}}{1} = \dfrac{{y + 5}}{1} = \dfrac{{z - 9}}{1} = \lambda $
Let this be equal to $\lambda $
So, here we can equate,
$
  \dfrac{{x - 1}}{1} = \lambda \\
  \dfrac{{y + 5}}{1} = \lambda \\
  \dfrac{{z - 9}}{1} = \lambda \\
 $
So,
$
  x = \lambda + 1 \\
  y = \lambda - 5 \\
  z = \lambda + 9 \\
 $
Here, $\left( {x,y,z} \right)$ lies on the plane $ABCD$ so it must satisfy the equation $x - y + z = 5$
So by putting $\left( {x,y,z} \right)$ values,
$
  \lambda + 1 - \lambda + 5 + \lambda + 9 = 5 \\
  \lambda = - 10 \\
 $
So now we get $\lambda = - 10$.
Now,
$
  x = \lambda + 1 = - 10 + 1 = - 9 \\
  y = \lambda - 5 = - 10 - 5 = - 15 \\
  z = \lambda + 9 = - 10 + 9 = - 1 \\
 $
So, we got, $Q\left( {x,y,z} \right) = \left( { - 9, - 15, - 1} \right)$
Now by distance formula, we can find $PQ$
$PQ = \sqrt {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2} + {{\left( {z - {z_1}} \right)}^2}} $
Here, $P\left( {{x_1},{y_1},{z_1}} \right) = \left( {1, - 5,9} \right)$
And $Q\left( {x,y,z} \right) = \left( { - 9, - 15, - 1} \right)$
So,
 $
  PQ = \sqrt {{{\left( { - 9 - 1} \right)}^2} + {{\left( { - 15 + 5} \right)}^2} + {{\left( { - 1 - 9} \right)}^2}} \\
   = \sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 10} \right)}^2} + {{\left( { - 10} \right)}^2}} \\
   = \sqrt {100 + 100 + 100} \\
   = \sqrt {300} \\
   = 10\sqrt 3 \\
 $
So, the distance of point $\left( {1, - 5,9} \right)$ from the plane $x - y + z = 5$ measured along the line $x = y = z$ is $10\sqrt 3 $.

So, the correct answer is “Option B”.

Note:If the equation of plane is given as $ax + by + cz + d = 0$ and only point $\left( {{x_1},{y_1},{z_1}} \right)$ is given, so the perpendicular distance of that point from plane $ax + by + cz + d = 0$ is given as
$\dfrac{{|a{x_1} + b{y_1} + c{z_1} + d|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$
This is valid when we need to find the perpendicular distance. If we need to find distance along any direction, then use the above method as stated.