Question

The distance between \[{{1}^{st}}\]crest and \[{{7}^{th}}\]trough of a transverse wave of wavelength 20cm is ______
A. 100
B. 110
C. 120
D. 130

Answer 1

Hint: Remember that a wave consists of a crest and a trough. Wavelength is the distance between two consecutive crests or two troughs. The length of a crest or trough is \[\dfrac{\lambda }{2}\]. Then count the number of waves between \[{{1}^{st}}\] crest and \[{{7}^{th}}\] trough and add.

Complete step-by-step answer:
A wave is the result of a disturbance in a system. It transfers energy to the surroundings. A wave consists of a crest and a trough. The perpendicular distance from the crest or the trough to the axis of propagation is the amplitude. The highest displacement of the wave above the axis of propagation is called the crest. And the highest displacement of the particle below the axis of propagation is called the trough. It is the lowest point of a wave.
One wave consists of a crest and a trough. Wavelength is the length of one wave. Then the length of a crest and a trough together gives the wavelength.
The wavelength is denoted by the letter\[\lambda \]. Or wavelength is equal to the distance between two successive crests or two consecutive troughs.
Then in the problem, it is given that
The wavelength of the wave, \[\lambda \]=20cm.
We have to find the distance between \[{{1}^{st}}\]crest and \[{{7}^{th}}\]trough. To calculate the distance, it will be best if we try to draw the graphical representation of the wave. Since it is a transverse wave, let us take the axis of propagation of the wave along the X-axis. And the vibration is along the Y-axis.

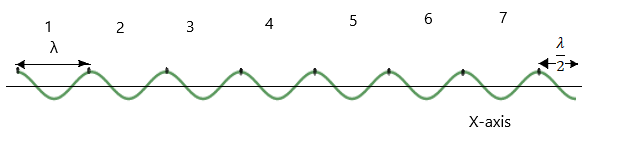
From the above figure, it is evident that there are six full waves and a one-half wave between the \[{{1}^{st}}\]crest and \[{{7}^{th}}\] trough.
Then let's do the calculations.
Length of the six waves = six times the wavelength .i.e.
Length of six waves = \[6\lambda \] …………….(1)
Length of one-half wave = \[\dfrac{\lambda }{2}\]……………………(2)
\[\therefore \] The total distance between \[{{1}^{st}}\]crest and \[{{7}^{th}}\]trough is equation (1) + equation (2)
i.e. =\[6\lambda +\dfrac{\lambda }{2}\]
= \[6\times 20+\dfrac{20}{2}\]
= \[120+10\]
\[=130\]cm
The total distance between \[{{1}^{st}}\]crest and \[{{7}^{th}}\]trough is 130cm.
Therefore option D is the answer.

Note: Remember since the wavelength is the measure of the length of one wave, its SI unit is meter. Length of a crest = length of one trough = \[\dfrac{\lambda }{2}\]. The unit of amplitude is also m. Whereas for frequency, it is \[{{s}^{-1}}\] or Hz. When you are confused to solve the problems like this, it will be helpful if you try to draw the figure.