Question

The difference between outside and inside surfaces of a cylindrical metallic pipe 14 cm long is 44 cm\[^2\]. If the pipe is made of 99 cm\[^3\] of metal, find the outer and inner radii of the pipe.

Answer 1

Hint: First we will first assume that the outer and inner radii of the pipe are \[R\] cm and \[r\] cm respectively and \[h\]is the height of the cylinder. We use the formula of the surface area of the cylinder is \[2\pi rh\], where \[r\] is the radius of the circle and \[h\] is the height of the cylinder to find the difference of the outside and inside surface area of a cylindrical pipe using the outer and inner radii. Then we will use the formula of the volume of the cylinder is \[\pi {r^2}h\], where \[r\] is the radius of the circle and \[h\] is the height of the cylinder to find the difference of the outside and inside volume of a cylindrical pipe using the outer and inner radii. Then substituting the values in the obtained equation to find the required values.

Complete step by step Answer:

We are given that the difference between outside and inside surfaces of a cylindrical metallic pipe 14 cm long is 44 cm\[^2\].

Let us assume that the outer and inner radii of the pipe are \[R\] cm and \[r\] cm respectively and \[h\]is the height of the cylinder.

We know that the formula to find the surface area of the cylinder is \[2\pi rh\], where \[r\] is the radius of the circle and \[h\] is the height of the cylinder

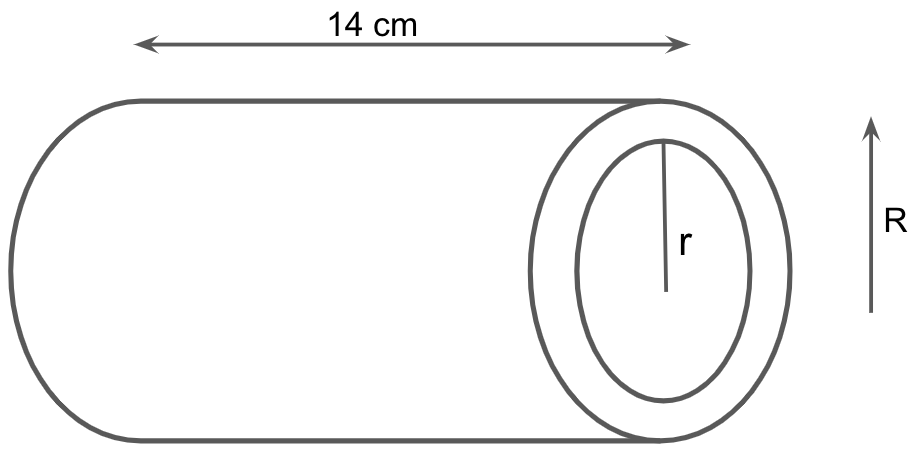
Finding the difference of the outside and inside surface area of a cylindrical pipe using the outer and inner radii, we get
\[
   \Rightarrow 2\pi R\left( {14} \right) - 2\pi r\left( {14} \right) = 44 \\
   \Rightarrow 28\pi R - 28\pi r = 44 \\
   \Rightarrow 28\pi \left( {R - r} \right) = 44 \\
 \]

Substituting the value of \[\pi \] in the above equation, we get
\[
   \Rightarrow 28 \times \dfrac{{22}}{7} \times \left( {R - r} \right) = 44 \\
   \Rightarrow 28 \times 22\left( {R - r} \right) = 44 \\
   \Rightarrow 88\left( {R - r} \right) = 44 \\
 \]

Dividing the above equation by 88 on both sides, we get
\[
   \Rightarrow \dfrac{{88\left( {R - r} \right)}}{{88}} = \dfrac{{44}}{{88}} \\
   \Rightarrow R - r = \dfrac{1}{2}{\text{ .......eq.(1)}} \\
 \]

We know that the formula to find the volume of the cylinder is \[\pi {r^2}h\], where \[r\] is the radius of the circle and \[h\] is the height of the cylinder

Since we are given that the pipe of metal is 99 cm cube, which is the volume of the pipe, by finding the difference of the outside and inside volume of a cylindrical pipe using the outer and inner radii, we get
\[
   \Rightarrow \pi {R^2}\left( {14} \right) - \pi {r^2}\left( {14} \right) = 99 \\
   \Rightarrow 14\pi \left( {{R^2} - {r^2}} \right) = 99 \\
 \]

Substituting the value of \[\pi \] in the above equation, we get
\[
   \Rightarrow 14 \times \dfrac{{22}}{7}\left( {{R^2} - {r^2}} \right) = 99 \\
   \Rightarrow 44\left( {{R^2} - {r^2}} \right) = 99 \\
 \]

Dividing the above equation by 44 on both sides, we get
\[
   \Rightarrow \dfrac{{44\left( {{R^2} - {r^2}} \right)}}{{44}} = \dfrac{{99}}{{44}} \\
   \Rightarrow {R^2} - {r^2} = \dfrac{9}{4} \\
   \Rightarrow \left( {R - r} \right)\left( {R + r} \right) = \dfrac{9}{4} \\
 \]

Using equation (1) in the above equation, we get
\[ \Rightarrow \dfrac{{R + r}}{2} = \dfrac{9}{4}\]

Multiplying the above equation by 2 on both sides, we get
\[ \Rightarrow R + r = \dfrac{9}{2}{\text{ ......eq.(2)}}\]

Adding the equation (1) and equation (2), we get
\[
   \Rightarrow R - r + R + r = \dfrac{1}{2} + \dfrac{9}{2} \\
   \Rightarrow 2R = \dfrac{{10}}{2} \\
   \Rightarrow 2R = 5 \\
 \]

Dividing the above equation by 2 on both sides, we get
\[
   \Rightarrow \dfrac{{2R}}{2} = \dfrac{5}{2} \\
   \Rightarrow R = \dfrac{5}{2}{\text{ cm}} \\
 \]

Substituting the value of \[R\] in the equation (2), we get
\[
   \Rightarrow \dfrac{5}{2} + r = \dfrac{9}{2} \\
   \Rightarrow r = \dfrac{9}{2} - \dfrac{5}{2} \\
   \Rightarrow r = \dfrac{4}{2} \\
   \Rightarrow r = 2{\text{ cm}} \\
 \]

Thus, the outer radius is \[\dfrac{5}{2}\] cm and the inner radius is 2 cm.

Note: In solving this type of question, the key concept is to assume the inner and outer radii by some distinct variables and also remember the formulae of the circumference of the circle, area of the cylinder, and the volume of the cylinder. After that, the question is really simple if followed properly.