Question

The diagram shows two arcs, A and B. Arc A is part of the circle with centre O and radius OP. Arc B is part of the circle with centre M and radius PM, where M is the midpoint of PQ. Show that the area enclosed by the two arcs is equal to $25\left( {\sqrt 3 - \dfrac{\pi }{6}} \right)c{m^2}.$

Answer 1

Hint- In this question, the radius of two arcs is given to us. We have to find the area enclosed by the two arcs, using a simple formula for area of semicircle and formula for area of segment of circle. Subtract both segments to get the required answer.

Complete step-by-step solution -

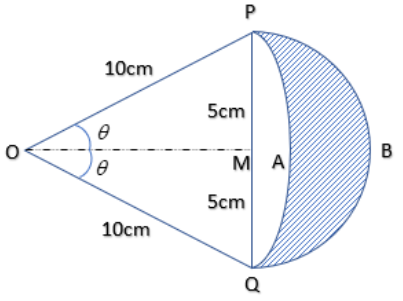
Area enclosed by arc B and chord PQ = Area of semicircle of radius 5cm $ = \dfrac{1}{2} \times \pi \times {(5cm)^2} = \dfrac{{25\pi }}{2}c{m^2}$
Let $\angle MOQ = \angle MOP = \theta $
Now, in $\Delta PMO,$
We know that, $\sin \theta = \dfrac{P}{H}$ where P = perpendicular and H = Hypotenuse in a right-angled triangle.
$\sin \theta = \dfrac{{PM}}{{OP}} = \dfrac{{5cm}}{{10cm}} = \dfrac{1}{2}$
$\therefore \theta = {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right)$
We know that ${\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) = {30^0}$
$ \Rightarrow \theta = {30^0}$
Area of segment of circle of radius 10cm containing angle $(2\theta = {60^0})$
$ = \dfrac{{\pi {r^2}\theta }}{{360}} = \dfrac{{\pi {{(10)}^2} \times {{60}^0}}}{{{{360}^0}}} = \dfrac{{100\pi }}{6}$
Area of \[\Delta POQ = \dfrac{{\sqrt 3 {{\left( {side} \right)}^2}}}{4} = \dfrac{{\sqrt 3 {{\left( {10cm} \right)}^2}}}{4} = \dfrac{{\sqrt 3 \times 100c{m^2}}}{4} = 25\sqrt 3 c{m^2}\]
Area enclosed by two arcs = Area enclosed by the arc B and chord PQ + area of $\Delta POQ$ - Area enclosed by arc A of radius 10cm
$ = \dfrac{{25\pi }}{2}c{m^2} + 25\sqrt 3 c{m^2} - \dfrac{{100\pi }}{6}c{m^2} = 25\sqrt 3 c{m^2} - \dfrac{{25\pi }}{6}c{m^2} = 25\left( {\sqrt 3 - \dfrac{\pi }{6}} \right)c{m^2}$
Hence, it has been showed that the area enclosed by the two arcs is equal to $25\left( {\sqrt 3 - \dfrac{\pi }{6}} \right)c{m^2}.$

Note- For these types of questions, always try to solve by analyzing the figure and whenever equilateral triangle shows appearance use its properties like area, internal angles etc. where area of equilateral triangle is \[\dfrac{{\sqrt 3 {{\left( {side} \right)}^2}}}{4}\] . Also, keep in mind that area of segment of circle containing an angle $\theta $ is $\dfrac{{\pi {r^2}\theta }}{{360}}$ and area of semicircle is equal to $\dfrac{{\pi {r^2}}}{2}$.