Question

The diagram shows the energy levels for an electron in a certain atom. Which transition shown represents the emission of a photon with the most energy?

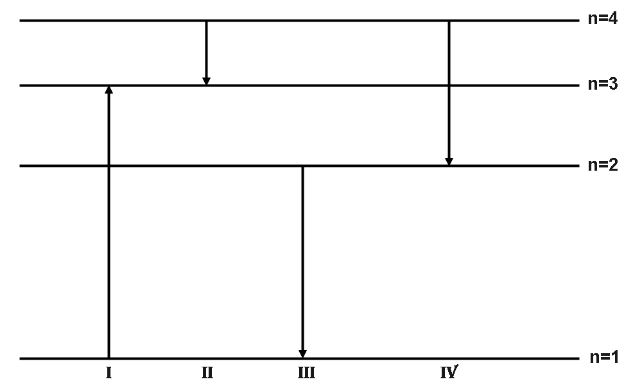
A. $I$
B. $II$
C. $III$
D. $IV$

Answer 1

Hint:To solve this question, we will use the formula to calculate Energy of emitted radiation, and we will verify each transition and the transition which will show the most energy after emission will be our required answer.

Formula used:
$E = Rhc\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right)$
Where, $R$ is the Rydberg’s constant, $h$ is Planck’s constant, $c$ is the speed of light, ${n_1}$ is the final state and ${n_2}$ is the initial state.

Complete step by step answer:
As we know that how to calculate Energy of emitted radiation,
$E = Rhc\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right)$
Now we will check simultaneously from each energy level that which transition shows the emission of a photon with the most energy.
At first, we will check from $4 \to 3$
$E = Rhc\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right) \\
\Rightarrow {E_{(4 \to 3)}} = Rhc\left( {\dfrac{1}{{{3^2}}} - \dfrac{1}{{{4^2}}}} \right) \\
\Rightarrow {E_{(4 \to 3)}} = Rhc\left( {\dfrac{7}{{9 \times 16}}} \right) \\
\Rightarrow {E_{(4 \to 3)}} = 0.05Rhc \\ $
Now, we will check from $2 \to 1$
$E = Rhc\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right) \\
\Rightarrow {E_{(4 \to 2)}} = Rhc\left( {\dfrac{1}{{{2^2}}} - \dfrac{1}{{{4^2}}}} \right) \\
\Rightarrow {E_{(4 \to 2)}} = Rhc\left( {\dfrac{3}{{16}}} \right) \\
\Rightarrow {E_{(4 \to 2)}} = 0.2Rhc \\ $
Now, we will check from $4 \to 1$
$E = Rhc\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right) \\
\Rightarrow {E_{(2 \to 1)}} = Rhc\left( {\dfrac{1}{{{1^2}}} - \dfrac{1}{{{2^2}}}} \right) \\
\Rightarrow {E_{(2 \to 1)}} = Rhc\left( {\dfrac{3}{4}} \right) \\
\Rightarrow {E_{(2 \to 1)}} = 0.75Rhc \\ $
Now, we will check from $1 \to 4$
$E = Rhc\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right) \\
\Rightarrow {E_{(1 \to 4)}} = Rhc\left( {\dfrac{1}{{{4^2}}} - \dfrac{1}{{{1^2}}}} \right) \\
\Rightarrow {E_{(1 \to 4)}} = Rhc\left( { - \dfrac{{15}}{{16}}} \right) \\
\therefore {E_{(1 \to 4)}} = - 0.9Rhc $
Thus, we can say that the transition represented by $III$ will emit the maximum energy photon.

Hence, the correct option is C.

Note:Note that to move an electron from the $n = 1$ to an excited state, the atom must absorb energy, depending upon the amount of energy the atom absorbs, an electron may go from$n = 1$ to $n = 2,3,4,...$ So, when the electron goes back to the ground state it releases energy corresponding to the difference in energy levels from final to initial.