Question

The diagram shows an unbalanced rod. Two loads X and Y can be moved along the rod. The rod turns in the clockwise direction as shown in the figure. Which action could make the rod balance?

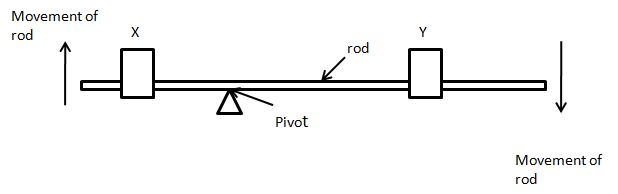
A) Moving X to the left
B) Moving X to the right
C) Moving Y to the right
D) Moving the pivot to the left

Answer 1

Hint: Determine the force which is responsible for rotation of the rod. If this force gets balanced, the rod will not move. For this to happen, the net torque on the above system should be zero.

Complete step by step answer:
We know that the rotation of the rod is caused due to torque acting on rod. The centre of rotation of the rod is at the position of pivot. The rotation of the rod is caused due to weight of box X and Y. Therefore, the weight of the boxes is the force responsible for the torque.

We can show the direction of weight of both boxes as shown in the figure below.

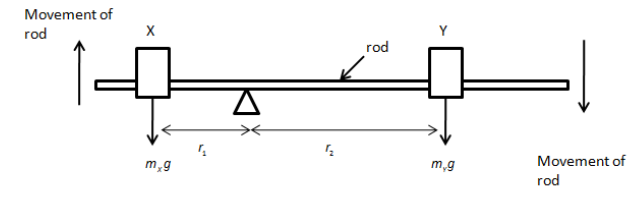
We know the torque responsible for the rotation due to weight of box Y is,
\[{\tau _2} = {m_Y}g{r_2}\]
Here, \[{r_1}\] is the distance between the pivot and point of weight of Y.

We also know the torque responsible for the rotation due to weight of box X is,
\[{\tau _1} = {m_X}g{r_1}\]
Here, \[{r_2}\] is the distance between the pivot and point of weight of X.

Therefore, we see that the net torque due to box Y is greater than that of box X, since the distance \[{r_2} > {r_1}\].
We have net torque on this system is,
\[{\tau _{net}} = {\tau _1} - {\tau _2}\]
The system will not rotate when the net torque on the system is zero. Therefore,
\[{\tau _1} - {\tau _2} = 0\]
\[ \Rightarrow {\tau _1} = {\tau _2}\]
We can see the torque \[{\tau _1}\] and \[{\tau _2}\] will be equal when the distance from the pivot is the same. Therefore, if we move the box X towards the left, the distance from the pivot will be the same for both boxes and the rod will not rotate.

Hence, the correct option is option (A).

Note:While solving this question we have assumed that the mass of the rod does not contribute to the torque but in reality the mass of the rod also contributes to the torque. The mass towards the right is the sum of mass of box Y and mass of rod towards the right from the pivot. Therefore, we don’t need to move box X at equal distance from pivot as that of box Y.