Question

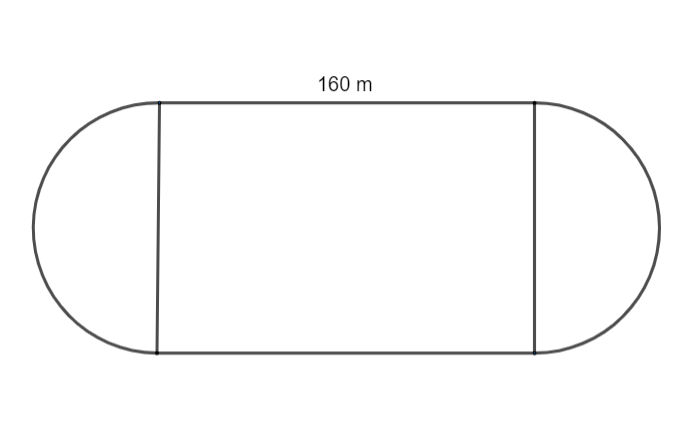
The diagram shows a track composed of a rectangle with a semicircle on each end. The area of the rectangle is 14,400 square meters. What is the perimeter of the track?

Answer 1

Hint: To solve the given problem, we should know the formula for calculating the area of the rectangle. The area of the rectangle equals the product of its length and breadth. For the given track diagram, we can say that the radius of the semicircles equals the half of breadth of the rectangle. Also, the perimeter of the given track equals the sum of twice the length of the rectangle and twice the circumference of the semicircle.

Complete step-by-step solution:

We are given that the area of the rectangle equals 14,400 square meters. From the given figure, the length of the rectangle equals 160 m. We know that the area of a rectangle equals the product of its length and breadth. Let’s say the breadth of the rectangle equals b.
\[\therefore 14,400=160b\]
Dividing both sides of the above equation by 160, and flipping the sides of the equation. We get
\[\Rightarrow b=90m\]
From the figure we can find the radius of the semicircle as half of the breadth of the rectangle. Thus, the radius equals \[\dfrac{90}{2}m=45m\].
We need to find the perimeter of the track. The perimeter of the track equals the sum of twice the length of the rectangle and twice the circumference of the semicircle. We will calculate these terms separately and add them.
The length of the track is given as 160 m, twice the length equals 320 m.
The circumference of a semicircle equals \[\pi r\], multiplying it by 2 we get \[2\pi r\]. We have the radius as 45 m. hence, get \[2\pi r=2\pi \times 45\approx 282.6m\]
Adding these two terms we get the perimeter of track as \[320m+282.6m=602.6m\].

Note: Here, we are already given the figure of the track. If the figure is not given, we should first make the figure. Using the figure makes it easier to solve these types of problems. Calculation mistakes should be avoided, also the formula for area and perimeter should be remembered.