Question

The diagram shows a solid formed by joining a hemisphere, of radius r cm, to a cylinder, of radius r cm and height h cm. The total height of the solid is \[18{\text{ }}cm\]and the surface area is \[205\pi c{m^2}.\]
Find the value of r and the value of h.

Answer 1

Hint: At first, we will calculate the total surface area of the solid given. For that we will use the formula,
Curved surface area of hemisphere \[ = {\text{ }}2\pi {r^2}\]
Surface area of cylinder \[ = \pi {r^2} + {\text{ }}2\pi rh\]
After putting the value in the above formulas and then on adding we will get the total surface area of the solid. Total height of the solid is also given, after using this value, we will get the value of r and h.

Complete step-by-step answer:

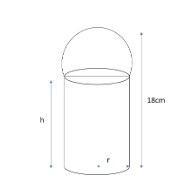
Step 1: We have been given total height of the solid \[ = {\text{ }}18{\text{ }}cm\]
And also, total surface area of the solid \[ = {\text{ }}205\pi c{m^2} \ldots \ldots eq.{\text{ }}\left( 1 \right)\]
Total surface area of solid \[ = \] Curved surface area of hemisphere \[ + \] Surface area of cylinder \[ = {\text{ }}2\pi {r^2} + \pi {r^2} + {\text{ }}2\pi r{h^{}} \ldots \ldots eq.{\text{ }}{\left( 2 \right)^{}}\]
On equating, \[eq.{\text{ }}\left( 1 \right)\] and \[eq.{\text{ }}\left( 2 \right),\]we get
\[\begin{array}{*{20}{l}}
  {3\pi {r^2} + {\text{ }}2\pi rh{\text{ }} = {\text{ }}205\pi } \\
  {3{r^2} + {\text{ }}2rh{\text{ }} = {\text{ }}205 \ldots ..eq.{\text{ }}\left( 3 \right)}
\end{array}\]
Step 2: Since, \[h{\text{ }} + {\text{ }}r{\text{ }} = {\text{ }}18{\text{ }}cm\] (given total height of the solid)
\[h{\text{ }} = {\text{ }}18{\text{ }}-{\text{ }}r\]
On putting the value of \[h{\text{ }} = {\text{ }}18{\text{ }}-{\text{ }}r{\text{ }}in{\text{ }}eq.{\text{ }}\left( 3 \right),\] we get
\[\begin{array}{*{20}{l}}
  {3{r^2} + {\text{ }}2r{\text{ }}\left( {18{\text{ }}-{\text{ }}r} \right){\text{ }} = {\text{ }}205} \\
  {3{r^2} + {\text{ }}36r{\text{ }}-{\text{ }}2{r^2} = {\text{ }}205} \\
  {{r^2} + {\text{ }}36r{\text{ }}-{\text{ }}205{\text{ }} = {\text{ }}0} \\
  {\left( {r{\text{ }} + {\text{ }}41} \right){\text{ }}\left( {r{\text{ }} - {\text{ }}5} \right){\text{ }} = {\text{ }}0} \\
  {r{\text{ }} = {\text{ }} - {\text{ }}41,{\text{ }}5}
\end{array}\]
Here, we will neglect, \[r = {\text{ }} - 41,{\text{ }}we{\text{ }}get{\text{ }}r{\text{ }} = {\text{ }}5{\text{ }}cm\]
Step 3: Now on putting the value of r in \[h{\text{ }} = {\text{ }}18{\text{ }}-{\text{ }}r,\]we get
\[h{\text{ }} = {\text{ }}18{\text{ }}-{\text{ }}5{\text{ }} = {\text{ }}13{\text{ }}cm\]
Thus, radius and height of the solid are \[5{\text{ }}cm\] and \[13{\text{ }}cm\]respectively.

Note: Students should take care, that here, we have neglected the negative value of r, as radius can’t be negative.