Question

The diagram shows a running track. The ‘ends’ of the track are semicircles.

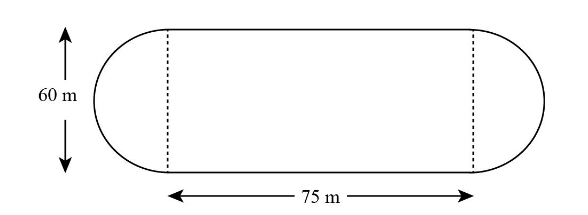
Philipe wants to run at least 4 km and must run a whole number of laps. What is the least number of laps he can run?

Answer 1

Hint: The number of laps around a running track should be calculated using the ratio of the distance covered to the perimeter of the running track i.e. $ {\text{Number of laps = }}\dfrac{{{\text{Total distance covered}}}}{{{\text{Perimeter of the running track}}}} $ . We must analyse the shape of the running track and then use the formula to calculate the perimeter of the shape/shapes of the running track. The perimeter of a rectangle can be given as twice the sum of the length and breadth of a rectangle. In addition to this, the perimeter of a circle is $ 2\pi r $ , where $ r $ is the radius of the circle.

Complete step-by-step answer:
The diagram shows that the running track is made of 2 semicircles and one rectangle. The semicircles are joined on both the ends of the rectangle.
The diameter of the semi-circular track in the diagram is given as 30 m i.e. . So, the radius is half the diameter.
 $
\Rightarrow r = \dfrac{d}{2}\\
 = \dfrac{{60}}{2}\\
 = 30
 $
Also, the length and breadth of the rectangular track is given as 75 m and 60 m.
Perimeters of the running track can be calculated by adding the perimeters of a circle and the rectangle.
Perimeter of a circle is given as $ 2\pi r $ , where $ r $ is the radius.
So, the perimeter of the 2 semicircles excluding the diameter is equal to the perimeter of the circle.
Perimeter of the circle is given as
 $ \Rightarrow {P_c} = 2\pi r $
After, substituting $ r = 30 $ and $ \pi = \dfrac{{22}}{7} $ , we get,
 $
\Rightarrow {P_c} = 2 \cdot \dfrac{{22}}{7} \cdot 30\\
 = 188.57
 $
The perimeter of a rectangle can be given as $ 2\left( {l + b} \right) $ , where $ l $ and $ b $ are the length and breadth of the rectangle respectively.
So, the perimeter of the rectangular shape is given as
 $ \Rightarrow {P_r} = 2\left( {l + b} \right) $
Perimeter of the diagram is the path which surrounds the two-dimensional figure. In the diagram, it can be seen that the breadth of the rectangle is not included as the path, so the breadth of the rectangle should not be included in the perimeter of the entire track.
So, the perimeter of the rectangle part will include twice of the length i.e. $ 2l = 2\left( {75} \right) $ i.e. 150 m.
 $
\Rightarrow {P_r} = 2 \cdot \left( {75} \right)\\
 = 150
 $
The perimeter of the entire track i.e. $ P $ is given by the sum of the perimeter of the rectangular part and the circular part.
 $ \Rightarrow {\text{P = }}{P_r} + {P_c} $
After substituting $ {P_c} = 188.57 $ and $ {P_r} = 150 $ in the equation $ {\text{P = }}{P_r} + {P_c} $ , we get,
 $
\Rightarrow P = 150 + 188.57\\
 = 338.57
 $
Philipe wants to cover at least 4 kms.
We known that $1{\text{ km = 1000 m}}$
So, $ 4{\text{ km = 4 }} \times {\text{ }}\left( {1{\text{ km}}} \right) $
After substituting $ 1{\text{ km = 1000 m}} $ in the equation $ 4{\text{ km = 4 }} \times {\text{ }}\left( {1{\text{ km}}} \right) $
 $
4{\text{ km = 4 }} \times {\text{ }}\left( {1000{\text{ m}}} \right)\\
 = 4000{\text{ m}}
 $
The total distance to be covered around the running track is 4000 m.
So, the number of laps can be calculated as the ratio of the total distance to be covered to the perimeter of the running track.
 $ \Rightarrow {\text{Number of laps = }}\dfrac{{{\text{Total distance covered}}}}{{{\text{Perimeter of the running track}}}} $
After substituting total distance covered as 4000 and perimeter of the running track as 338.57, we get,
 $
{\text{Number of laps = }}\dfrac{{{\text{4000}}}}{{338.57}}\\
 = 11.81
 $
Therefore, Philipe can run at least 11 laps
So, the correct answer is “11”.

Note: In this type of question, students should take utmost care while calculating the perimeter of the running track. If the running track is in the form of a circle, we can use $ 2\pi r $ as the perimeter. Also, if the running track is in the form of a rectangle, we can use $ 2\left( {l + b} \right) $ as the perimeter. But while calculating the perimeter of a running track with a combination of different geometric shapes, at that time only the definition of the perimeter comes handy. Students should apply the definition of the perimeter to the given shape of the running track.