Question

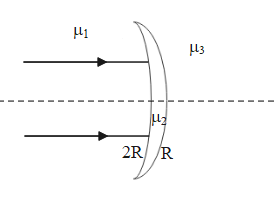
The diagram shows a concavo-convex lens with refractive index ${{\mu }_{2}}$. What is the condition on the refractive indices so that the lens is diverging?

A. $2{{\mu }_{3}}<{{\mu }_{1}}+{{\mu }_{2}}$
B. $2{{\mu }_{3}}>{{\mu }_{1}}+{{\mu }_{2}}$
C. ${{\mu }_{3}}>2\left( {{\mu }_{1}}+{{\mu }_{2}} \right)$
D. None of these

Answer 1

Hint: Use the equation for the refraction at a spherical interface of two different mediums at both the interfaces by considering an intermediate image. Final an expression for the position of the final image and put the condition for the lens to be diverging.

Complete step by step answer:
 The equation of the refraction of light at a spherical interface of two different mediums is given as $\dfrac{{{\mu }_{r}}}{v}-\dfrac{{{\mu }_{i}}}{u}=\dfrac{{{\mu }_{r}}-{{\mu }_{i}}}{R}$ ….. (i).
Here, ${{\mu }_{i}}$ is the refractive index of the medium from which the light ray is incident on the interface and ${{\mu }_{r}}$ is the refractive index of the medium in which the light ray enters after refraction. v and u are the positions of the image and the object with respect to the lens. R is the radius of curvature of the spherical interface.
The values of u, v and R are according to the sign convection.
In the given case, the light will first refract at the concave side. Due to this an intermediate image is formed at v’. This intermediate image now acts as an object for the refraction at the convex side and a final image is formed at v.
Let the equation of refraction for the first case.
We can see that the light rays are coming from infinity. This means that the object is placed at infinity.
$\Rightarrow u=\infty $.
And $v=v'$.
Here, ${{\mu }_{i}}={{\mu }_{1}}$ , ${{\mu }_{r}}={{\mu }_{2}}$ and the radius of curvature of the concave part is 2R. Therefore, $R=-2R$.
After substituting the values in equation (i), we get
$\dfrac{{{\mu }_{2}}}{v'}-\dfrac{{{\mu }_{1}}}{\infty }=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{-2R}$
$\dfrac{{{\mu }_{2}}}{v'}-0=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{-2R}$ ….. (iii).
Now, let us find the equation for the refraction at the convex surface.
For, $u=v'$, ${{\mu }_{i}}={{\mu }_{2}}$ , ${{\mu }_{r}}={{\mu }_{3}}$ and $R=-R$.
Substitute the values in (i).
$\Rightarrow \dfrac{{{\mu }_{3}}}{v}-\dfrac{{{\mu }_{2}}}{v'}=\dfrac{{{\mu }_{3}}-{{\mu }_{2}}}{-R}$ …. (iii).
Now, add (ii) and (iii).
$\Rightarrow \dfrac{{{\mu }_{3}}}{v}=\dfrac{{{\mu }_{2}}-{{\mu }_{1}}}{-2R}+\dfrac{{{\mu }_{3}}-{{\mu }_{2}}}{-R}$
$\Rightarrow \dfrac{{{\mu }_{3}}}{v}=\dfrac{{{\mu }_{1}}-{{\mu }_{2}}}{2R}+\dfrac{{{\mu }_{2}}-{{\mu }_{3}}}{R}$
$\Rightarrow \dfrac{{{\mu }_{3}}}{v}=\dfrac{{{\mu }_{1}}-{{\mu }_{2}}+2\left( {{\mu }_{2}}-{{\mu }_{3}} \right)}{2R}$
$\Rightarrow \dfrac{{{\mu }_{3}}}{v}=\dfrac{{{\mu }_{1}}+{{\mu }_{2}}-2{{\mu }_{3}}}{2R}$.
However, the condition on the lens is that it must be diverging. Therefore, the image will be formed on the same side of the object. Thus, the value of v is negative.
This implies that $\dfrac{{{\mu }_{3}}}{v}<0$.
$\Rightarrow \dfrac{{{\mu }_{1}}+{{\mu }_{2}}-2{{\mu }_{3}}}{2R}<0$
Since R is positive, ${{\mu }_{1}}+{{\mu }_{2}}-2{{\mu }_{3}}<0$.
$\Rightarrow 2{{\mu }_{3}}>{{\mu }_{1}}+{{\mu }_{2}}$
Hence, we found the condition on the refractive indices such that the lens becomes diverging.

So, the correct answer is “Option B”.

Note:
When the object is infinity or the rays of light are parallel to the optical axis, the point on the axis where the image is formed is called the focal of the lens. The position of the focus form the lens is called the focal length (f).
Therefore, in this case $f=v$.
 And for a diverging lens focal length is always negative.