Question

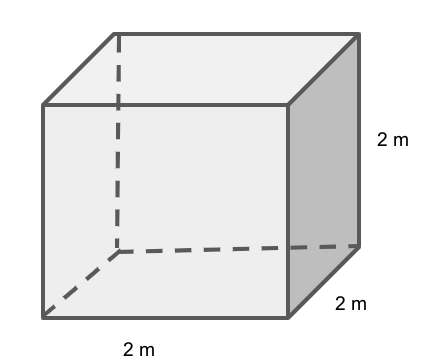
The diagram shows a box in the shape of a cube of lengths 2 m. The box is packed with cubes of lengths 1 cm. How many cubes does it hold?

A.8000
B.8000000
C.4000000
D.40000

Answer 1

Hint: Here, we will assume that the smaller cubes are arranged evenly inside the bigger cube such that no empty space inside the bigger cube. Then we will compute the volume of the bigger cube using the formula of the volume of the cube is \[{l^3}\], where \[l\] is the length of the side. Then let us assume that the total number of small cubes is \[x\] and use the given conditions to find the required value.

Complete step-by-step answer:
We are given that a box is in the shape of a cube with length 2 m and the box is packed with cubes of length 1 cm.
We have to assume that the smaller cubes are arranged evenly inside the bigger cube such that no empty space is inside the bigger cube.
So we know that the total volume of smaller cubes will be equal to the volume of the bigger cube.
First, we will compute the volume of the bigger cube.
We know that the formula of the volume of the cube is \[{l^3}\], where \[l\] is the length of the side.
Using the above formula of volume to find the volume of the bigger cube with side 2 m, we get
\[ \Rightarrow {\left( 2 \right)^3} = 8{\text{ }}{{\text{m}}^3}\]
Converting the above value into centimeters using the scale \[1{\text{ }}{{\text{m}}^3} = {10^6}{\text{ c}}{{\text{m}}^3}\], we get
\[ \Rightarrow 8 \times {10^6}{\text{ c}}{{\text{m}}^3}\]
Let us assume that the total number of small cubes is \[x\].
Using the above formula of volume to find the volume of the smaller cube with side 1 cm, we get
\[ \Rightarrow {\left( 1 \right)^3} = 1{\text{ c}}{{\text{m}}^3}\]
Multiplying the above value with \[x\]to find the total volume of \[x\] small cubes, we get
\[ \Rightarrow 1{\text{ c}}{{\text{m}}^3} \times x = x{\text{ c}}{{\text{m}}^3}\]
Since, the volume of smaller cubes will be equal to one bigger cube, we get
\[
   \Rightarrow x{\text{ c}}{{\text{m}}^3} = 8 \times {10^6}{\text{ c}}{{\text{m}}^3} \\
   \Rightarrow x = 8 \times {10^6} \\
   \Rightarrow x = 8000000 \\
 \]
Therefore, option b is correct.

Note: When we are computing the volumes of any shape we must take care of the unit. We know that if the units are the same then volumes can be directly equated, whereas if different then need to be converted first.