Question

The diagonal of a cube $ 4\sqrt 3 $ cm. What is the volume of the cube?

Answer 1

Hint: The longer diagonal of a cube of side $ a $ is $ a\sqrt 3 $ . The value should be compared with the standard value of a diagonal expressed in terms of its side. After calculating the side, the value can be calculated using the formula for volume of the cube as $ {a^3} $ , where $ a $ is the side length of a cube.

Complete step-by-step answer:
The given information is
Diagonal of a cube is, $ d = 4\sqrt 3 {\text{ cm}} $ .
Let us assume the diagonal is an internal longer diagonal.
The figure given below shows a cube of side length $ a $ cm.

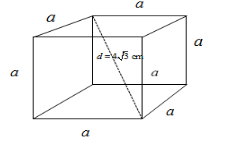
In order to calculate the volume of the cube, the side length of the cube is to be obtained.
The relation between the diagonal of a cube of side length units and diagonal $ d $ units is,
 $ d = a\sqrt 3 \cdots \left( 1 \right) $
Comparing the value of the diagonal given in the question $ d = 4\sqrt 3 $ with the diagonal in equation (1), we get the side length of the cube as,
Therefore, $ a = 4{\text{ cm}} $ .
Now, after calculating the side length of the cube it’s volume can be calculated using the formula
Volume of a cube,
 $ V = {a^3} \cdots \left( 2 \right) $
Substitute the value of the side length of a cube $ a = 4 $ in equation (2), we get
 $
\Rightarrow V = {4^3}{\text{ }} \\
\Rightarrow V = 64{\text{ c}}{{\text{m}}^3} \;
  $
Hence, the volume of the cube is $ V = 64 $ cubic cm. whose longer diagonal is $ 4\sqrt 3 {\text{ cm}} $ .
So, the correct answer is “$ V = 64 $ cubic. cm”.

Note: The important point in the question is to remember the formula for the diagonal of the cube in terms of its side as $ x\sqrt 3 $ where $ x $ is the side length of the cube. It is not given which diagonal it is, face diagonal or internal longer diagonal. As the value given in the question corresponds to the internal diagonal, so we have used the formula for the internal longer diagonal.