
The density of a rod having length $l$ varies as $\rho =c+Dx$, where $x$ is the distance from the left end. The centre of the mass is:
(A). $\dfrac{3cl+2D{{l}^{2}}}{3(2c+Dl)}$
(B). $\dfrac{2cl+3D{{l}^{2}}}{2(4c+8l)}$
(C). $\dfrac{2cl+3D{{l}^{2}}}{3(2c+l)}$
(D). $\dfrac{cl+D{{l}^{2}}}{3(2c+Dl)}$

Answer
566.4k+ views
Hint: The centre of mass of a body is a point at which the total mass of a body is assumed to be concentrated. The sum of product of mass and position of each point mass divided by the sum of all masses gives position of centre of mass. Since the density of the rod is varying with x. We integrate to determine the distribution of mass and hence find the centre of mass.
Formulae used:
${{X}_{cm}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}+......+{{m}_{n}}{{x}_{n}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+.....+{{m}_{n}}}$
$\rho =\dfrac{M}{V}$
Complete step-by-step solution:
The centre of mass is defined as the point on a body where the weighted relative positions of all point masses sums up to zero. This is a hypothetical point where the whole mass is assumed to be concentrated to simplify calculations when an object is in motion.
The formula of position of centre of mass is given by-
${{X}_{cm}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}+......+{{m}_{n}}{{x}_{n}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+.....+{{m}_{n}}}$
Here $\sum\limits_{1}^{n}{{{m}_{n}}{{x}_{n}}}$ is the product of mass and position of point masses.
$\sum\limits_{1}^{n}{{{m}_{n}}}$ is the sum of masses of all point objects
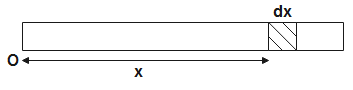
Given the density of rod is-$\rho =c+Dx$
The density ($\rho $) is defined as mass per unit volume, i.e.
$\rho =\dfrac{M}{V}$
Here,
$M$ is the mass of the object
$V$ is its volume
$\begin{align}
& \rho =c+Dx \\
& \Rightarrow \dfrac{M}{V}=c+Dx \\
& \Rightarrow \dfrac{M}{Adx}=c+Dx \\
\end{align}$
$\therefore M=Adx(c+Dx)$ ----------- (1)
For the centre of mass of the rod, we have,
$\begin{align}
& {{X}_{cm}}=\dfrac{\int\limits_{0}^{l}{Adx(cx+D{{x}^{2}})}}{\int\limits_{0}^{l}{Adx(c+Dx)}} \\
& \Rightarrow {{X}_{cm}}=\dfrac{A\int\limits_{0}^{l}{(cx+D{{x}^{2}})dx}}{A\int\limits_{0}^{l}{(c+Dx)dx}} \\
& \Rightarrow {{X}_{cm}}=\dfrac{\left[ c\dfrac{{{x}^{2}}}{2}+D\dfrac{{{x}^{3}}}{3} \right]_{0}^{l}}{\left[ cx+D\dfrac{{{x}^{2}}}{2} \right]_{0}^{l}} \\
\end{align}$
$\therefore {{X}_{cm}}=\dfrac{3cl+2D{{l}^{2}}}{3(2c+Dl)}$
Therefore, the centre of mass is situated at $\dfrac{3cl+2D{{l}^{2}}}{3(2c+Dl)}$.
Therefore, the correct option is (A).
Note:
Everybody is assumed to be a collection of point masses. In case of rigid bodies, the centre of mass is always fixed and in case of bodies with uniform distribution of mass, the centre of mass lies at the centre or very close to the centre. The velocity or acceleration of the whole body is equal to that of the centre of mass.
Formulae used:
${{X}_{cm}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}+......+{{m}_{n}}{{x}_{n}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+.....+{{m}_{n}}}$
$\rho =\dfrac{M}{V}$
Complete step-by-step solution:
The centre of mass is defined as the point on a body where the weighted relative positions of all point masses sums up to zero. This is a hypothetical point where the whole mass is assumed to be concentrated to simplify calculations when an object is in motion.
The formula of position of centre of mass is given by-
${{X}_{cm}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}+......+{{m}_{n}}{{x}_{n}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+.....+{{m}_{n}}}$

Here $\sum\limits_{1}^{n}{{{m}_{n}}{{x}_{n}}}$ is the product of mass and position of point masses.
$\sum\limits_{1}^{n}{{{m}_{n}}}$ is the sum of masses of all point objects
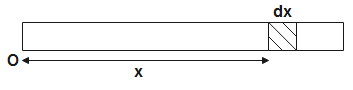
Given the density of rod is-$\rho =c+Dx$
The density ($\rho $) is defined as mass per unit volume, i.e.
$\rho =\dfrac{M}{V}$
Here,
$M$ is the mass of the object
$V$ is its volume
$\begin{align}
& \rho =c+Dx \\
& \Rightarrow \dfrac{M}{V}=c+Dx \\
& \Rightarrow \dfrac{M}{Adx}=c+Dx \\
\end{align}$
$\therefore M=Adx(c+Dx)$ ----------- (1)
For the centre of mass of the rod, we have,
$\begin{align}
& {{X}_{cm}}=\dfrac{\int\limits_{0}^{l}{Adx(cx+D{{x}^{2}})}}{\int\limits_{0}^{l}{Adx(c+Dx)}} \\
& \Rightarrow {{X}_{cm}}=\dfrac{A\int\limits_{0}^{l}{(cx+D{{x}^{2}})dx}}{A\int\limits_{0}^{l}{(c+Dx)dx}} \\
& \Rightarrow {{X}_{cm}}=\dfrac{\left[ c\dfrac{{{x}^{2}}}{2}+D\dfrac{{{x}^{3}}}{3} \right]_{0}^{l}}{\left[ cx+D\dfrac{{{x}^{2}}}{2} \right]_{0}^{l}} \\
\end{align}$
$\therefore {{X}_{cm}}=\dfrac{3cl+2D{{l}^{2}}}{3(2c+Dl)}$
Therefore, the centre of mass is situated at $\dfrac{3cl+2D{{l}^{2}}}{3(2c+Dl)}$.
Therefore, the correct option is (A).
Note:
Everybody is assumed to be a collection of point masses. In case of rigid bodies, the centre of mass is always fixed and in case of bodies with uniform distribution of mass, the centre of mass lies at the centre or very close to the centre. The velocity or acceleration of the whole body is equal to that of the centre of mass.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




