Question

The current voltage relationship of a diode is $I = {I_0}[\exp (\dfrac{{eV}}{{KT}}) - 1]$ where $e$ the charge on electron is, $V$ is voltage applied, $K$ is Boltzmann constant, and $T$ is the temperature in Kelvin. Find the resistance of the diode if ${I_0} = 1.5\,mA$ and $T = 398\,K$.

Answer 1

Hint:In semiconductor devices, a PN junction diode is a very simple semiconductor device which permits the flow of current in only one direction by applying a reverse bias across negative side and hence depletion layer width increases.

Complete step by step answer:
As we have given the current and voltage relation of pn Junction diode as $I = {I_0}[\exp (\dfrac{{eV}}{{KT}}) - 1]$ and we will take the derivative of given current with voltage and since, ${I_0}$ is the maximum current which is constant which is given to us
${I_0} = 1.5\,mA$
Temperature is also a constant term which is given to us
$T = 398\,K$
And $e$ is the charge on electron which has a value of
$e = 1.6 \times {10^{ - 19}}C$
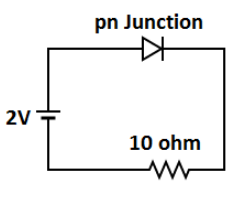
$Voltage = 2V$ Which is given in the circuit diagram.

Now, let us take the derivative current with respect to voltage which can be written as
$I = {I_0}[\exp (\dfrac{{eV}}{{KT}}) - 1]$
Take derivative as $\dfrac{{dI}}{{dV}}$
$\dfrac{{dI}}{{dV}} = {I_0}[(\dfrac{e}{{KT}})\exp (\dfrac{{eV}}{{KT}}) - 0]$
$\Rightarrow \dfrac{{dI}}{{dV}} = {I_0}(\dfrac{e}{{KT}}) \times \exp (\dfrac{{eV}}{{KT}})$
First, let us find the magnitude of $\exp (\dfrac{{eV}}{{KT}})$ by putting values of given parameters
$\exp (\dfrac{{eV}}{{KT}}) = \exp (\dfrac{{1.6 \times {{10}^{ - 19}} \times 2}}{{1.38 \times {{10}^{ - 23}} \times 398}})$
\[\Rightarrow \exp (\dfrac{{eV}}{{KT}}) = 1.88 \\ \]
And now, find the magnitude of ${I_0}(\dfrac{e}{{KT}})$
${I_0}(\dfrac{e}{{KT}}) = \dfrac{{1.5 \times {{10}^{ - 3}} \times 1.6 \times {{10}^{ - 19}}}}{{1.38 \times {{10}^{ - 23}} \times 398}}$
$\Rightarrow {I_0}(\dfrac{e}{{KT}}) = 0.04$
Now, put these two parameters value in equation $\dfrac{{dI}}{{dV}} = {I_0}(\dfrac{e}{{KT}}) \times \exp (\dfrac{{eV}}{{KT}})$
$\dfrac{{dI}}{{dV}} = 0.04 \times 1.88$
$\Rightarrow \dfrac{{dI}}{{dV}} = \dfrac{{15}}{{250}}$
Taking reciprocal of above equation we get
$\dfrac{{dV}}{{dI}} = \dfrac{{250}}{{15}}$
$\therefore \dfrac{{dV}}{{dI}} = \dfrac{{50}}{3}$
Since we know that $R = \dfrac{V}{I}$

Hence, $\dfrac{{dV}}{{dI}} = \dfrac{{50}}{3}$ is the resistance of the diode.

Hence, resistance of the diode is $16.67\Omega $.

Note: It should be remembered that, the basic conversions of units are as $1\,mA = {10^{ - 3}}\,A$ which a unit of current is and the relation between current, voltage and resistance $R = \dfrac{V}{I}$ is known as Ohm’s law. Since, external resistance and diode are connected in series hence the same current follows through both the resistor and diode but the voltage across the series components in the electric circuit is never the same it gets distributed but incase of parallel components voltage is same in both components of the circuit.