Question

The current drawn $5V$ source in the given circuit will be:

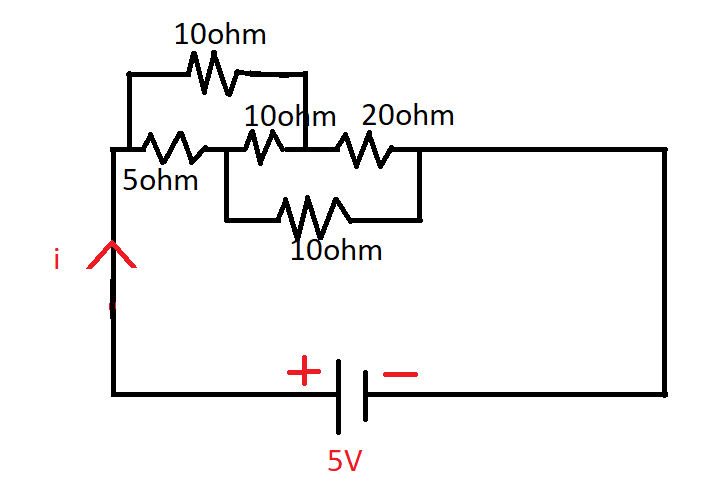
A. $0.33A$
B. $0.5A$
C. $0.67A$
D. $0.17A$

Answer 1

Hint: We already steadied that current is the rate of flow of charges. According to Ohm’s law across the circuit is proportional to the current across the circuit provided temperature, pressure, etc must be constant. So, from Ohm’s law, we got a relation between the current and voltage. Using this, we will calculate the current through the given circuit.

Complete step by step solution:
To solve the given circuit we first have to find the equivalent resistance of the circuit. Here, we can see that resistances are neither in series combination nor in parallel combination. And five resistances are there, so let us first check for Wheatstone bridge condition, if it follows.
A standard Wheatstone bridge is shown in the figure.

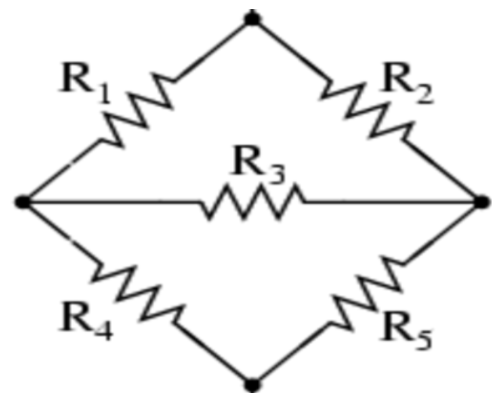
The balanced condition of the Wheatstone bridge is:
$\dfrac{{{R_2}}}{{{R_1}}} = \dfrac{{{R_5}}}{{{R_4}}} \Rightarrow {R_2}{R_4} = {R_1}{R_5}$
$ \Rightarrow \dfrac{{10}}{5} = \dfrac{{20}}{{10}} \Rightarrow 2 = 2$
Hence, it satisfies the Wheatstone bridge condition. So, it means no current flows in $10\Omega $(resistor in the middle) resistor and we can remove it. Now, the remaining resistances can be solved by either in series combination or parallel combination of resistors.
Series equivalent of $10\Omega $ and $20\Omega $ : $10 + 20 = 30\Omega $
Series equivalent of $5\Omega $and $10\Omega $ : $5 + 10 = 15\Omega $
Now, these two resistances, $30\Omega $and $15\Omega $are in parallel. So, their parallel equivalent :
${R_{eq}} = \dfrac{{30 \times 15}}{{30 + 15}} = \dfrac{{450}}{{45}} = 10\Omega $
Hence, the equivalent resistance of the circuit is $10\Omega $.
Now, let us use Ohm’s law to find the current in the circuit.
$V = IR \Rightarrow I = \dfrac{V}{R}$
$ \Rightarrow I = \dfrac{5}{{10}} = 0.5A$
Hence, option (B) $0.5A$ is correct.

Note:
Whenever a combination of 5 resistance is present and they are neither in parallel combination nor in series combination. We will use the Wheatstone bridge concept.
The equivalent of the series combination is the algebraic sum of all resistances.
${R_{eq}} = {R_1} + {R_2}$
The equivalent of the parallel combination is given by the following formula.
${R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$