
The cost price of an article is \[90\% \] of its selling price. What is the profit or the loss as a percentage?
A) \[10{1}{9}\% \] loss
B) \[11\dfrac{1}{9}\% \] profit
C) \[9\dfrac{1}{9}\% \] loss
D) \[12\dfrac{1}{9}\% \] profit
Answer
576k+ views
Hint: Here, we will assume the selling price and then find the cost price from the selling price. We will first check if the costing price is greater than the selling price, then compute the profit or loss by the difference of cost price and selling price. Then we will find the gain or loss percentage using \[{\text{Loss or Gain}}\% = \dfrac{{{\text{Loss or Gain}}}}{{{\text{C.P.}}}} \times 100\] from the given values to find the required value.
Complete step by step solution:
Let us assume that the selling price of an article \[{\text{S.P.}}\] is \[x\].
We will now find the cost price \[{\text{C.P.}}\] of the given article in terms of selling price \[x\].
\[
{\text{C.P.}} = \dfrac{{90}}{{100}} \times x \\
= 0.9x \\
\]
Thus, the cost price of an article is \[0.9x\].
Since we know that the selling price is greater than the cost price, there is a profit.
We know that the profit is calculated by the difference in the cost price of an article from selling price of an article.
Subtracting the values of cost price \[{\text{C.P.}}\] from the selling price \[{\text{S.P.}}\] to find the profit of a given article, we get
\[
{\text{Profit}} = x - 0.9x \\
= 0.1x \\
\]
We know that the formula to calculate the profit percentage is calculated as \[{\text{Profit}}\% = \dfrac{{{\text{Profit}}}}{{{\text{C.P.}}}} \times 100\], where C.P. is the cost price.
Substituting the values of Profit and C.P. in the above formula for profit percentage of the given article, we get
\[
{\text{Profit}}\% = \dfrac{{0.1x}}{{0.9x}} \times 100 \\
= \dfrac{1}{9} \times 100 \\
= \dfrac{{100}}{9}\% \\
\]
Simplifying the above fraction to find the profit percentage, we get
\[{\text{Profit}}\% = 11\dfrac{1}{9}\% \]
Thus, we get that the profit from an article is \[11\dfrac{1}{9}\% \].
Hence, the option is B will be correct.
Note:
Note: In these types of questions, students must assume the selling price as any variable and then find the cost price in terms of the selling price. We will find out gain or loss by comparing the selling price and the cost price. When the selling price is greater than the cost price, there is profit and when the cost price is greater than the selling price, there is a loss. We will find the final fraction by dividing the 100 by 9.
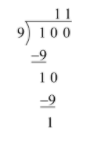
Writing it into the mixed fraction, \[{\text{Quotient}}\dfrac{{{\text{Remainder}}}}{{{\text{Divisor}}}}\] to match with the options, we get
\[11\dfrac{1}{9}\]
Complete step by step solution:
Let us assume that the selling price of an article \[{\text{S.P.}}\] is \[x\].
We will now find the cost price \[{\text{C.P.}}\] of the given article in terms of selling price \[x\].
\[
{\text{C.P.}} = \dfrac{{90}}{{100}} \times x \\
= 0.9x \\
\]
Thus, the cost price of an article is \[0.9x\].
Since we know that the selling price is greater than the cost price, there is a profit.
We know that the profit is calculated by the difference in the cost price of an article from selling price of an article.
Subtracting the values of cost price \[{\text{C.P.}}\] from the selling price \[{\text{S.P.}}\] to find the profit of a given article, we get
\[
{\text{Profit}} = x - 0.9x \\
= 0.1x \\
\]
We know that the formula to calculate the profit percentage is calculated as \[{\text{Profit}}\% = \dfrac{{{\text{Profit}}}}{{{\text{C.P.}}}} \times 100\], where C.P. is the cost price.
Substituting the values of Profit and C.P. in the above formula for profit percentage of the given article, we get
\[
{\text{Profit}}\% = \dfrac{{0.1x}}{{0.9x}} \times 100 \\
= \dfrac{1}{9} \times 100 \\
= \dfrac{{100}}{9}\% \\
\]
Simplifying the above fraction to find the profit percentage, we get
\[{\text{Profit}}\% = 11\dfrac{1}{9}\% \]
Thus, we get that the profit from an article is \[11\dfrac{1}{9}\% \].
Hence, the option is B will be correct.
Note:
Note: In these types of questions, students must assume the selling price as any variable and then find the cost price in terms of the selling price. We will find out gain or loss by comparing the selling price and the cost price. When the selling price is greater than the cost price, there is profit and when the cost price is greater than the selling price, there is a loss. We will find the final fraction by dividing the 100 by 9.
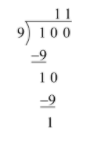
Writing it into the mixed fraction, \[{\text{Quotient}}\dfrac{{{\text{Remainder}}}}{{{\text{Divisor}}}}\] to match with the options, we get
\[11\dfrac{1}{9}\]
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

What are gulf countries and why they are called Gulf class 8 social science CBSE





