
The coordinates of the orthocenter of the triangle that has the coordinates of midpoints of its sides as \[\left( {0,{\text{ }}0} \right),{\text{ }}\left( {1,{\text{ }}2} \right)\]and \[\left( { - 6,{\text{ }}3} \right)\] is:
\[
A.\left( {0,{\text{ }}0} \right) \\
B.\left( { - 4,{\text{ }}5} \right) \\
C.\left( { - 5,{\text{ }}5} \right) \\
\]
Answer
577.8k+ views
Hint: At first using the midpoint formula we’ll find the coordinates of the vertices of the triangle. After getting the vertices of the triangle, we’ll find the length of the sides of the triangle using the distance formula.
Once we get the sides of the triangle, we try to find if the triangle is an equilateral or right-angled triangle for the easy approach for the solution.
Complete step-by-step answer:
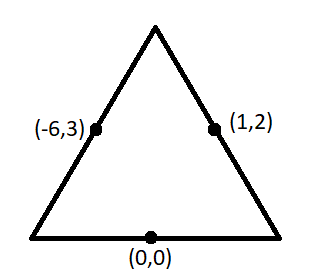
Given data: Mid-points of the sides of the triangle as \[\left( {0,{\text{ }}0} \right),{\text{ }}\left( {1,{\text{ }}2} \right)\] and \[\left( { - 6,{\text{ }}3} \right)\]
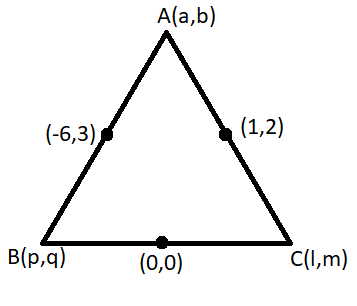
Let the triangle be ABC with the vertices as A(a, b), B(p, q), and C(l,m), i.e.
If the point (x, y) is the midpoint of $\left( {{x_1},{y_1}} \right)$and $\left( {{x_2},{y_2}} \right)$
Then, $x = \dfrac{{{x_1} + {x_2}}}{2}$
And $y = \dfrac{{{y_1} + {y_2}}}{2}$
Using this midpoint formula on side BC,
$ \Rightarrow \dfrac{{p + l}}{2} = 0$
$ \Rightarrow p = - l$,
and $\dfrac{{q + m}}{2} = 0$
$ \Rightarrow q = - m$
Using the midpoint formula on side AB,
$ \Rightarrow \dfrac{{a + p}}{2} = - 6$
$ \Rightarrow a + p = - 12...............(i),$
And $\dfrac{{b + q}}{2} = 3$
$ \Rightarrow b + q = 6................(ii)$
Using the midpoint formula on side CA,
$ \Rightarrow \dfrac{{l + a}}{2} = 1$
$ \Rightarrow l + a = 2................(iii)$,
And $\dfrac{{m + b}}{2} = 2$
$ \Rightarrow m + b = 4....................(iv)$
Substituting the value of ‘p’ in equation(i)
i.e.$a - l = - 12............(v)$
Substituting the value of ‘q’ in equation(ii)
i.e.$b - m = 6............(vi)$
now adding equation(iii) and (v)
i.e. $2a = - 10$
$\therefore a = - 5$
Substituting $a = - 5$in equation(v)
i.e., $l = 12 - 5$
$\therefore l = 7$
Since, $p = - l$
$\therefore p = - 7$
now adding equation(iv) and (vi)
i.e. $2b = 10$
$\therefore b = 5$
Substituting $b = 5$in equation(vi)
i.e., $m = 5 - 6$
$\therefore m = - 1$
Since, $q = - m$
$\therefore q = 1$
From the values of a,b,p,q,l,m we can say that the vertices of triangle ABC are
A(-5,5), B(-7,1), and C(7,-1)
Distance between two points U$\left( {{x_1},{y_1}} \right)$and V$\left( {{x_2},{y_2}} \right)$ is given by
$UV = \sqrt {{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2}} $
$ \Rightarrow U{V^2} = {({x_1} - {x_2})^2} + {({y_1} - {y_2})^2}$
On substituting values of A(-5,5) and B(-7,1), we get
$\therefore A{B^2} = {( - 5 + 7)^2} + {(5 - 1)^2}$
On simplifying we get,
$ \Rightarrow A{B^2} = 4 + 16$
$ \Rightarrow A{B^2} = 20$
Again using the distance formula on B(-7,1), and C(7,-1)
$i.e.,B{C^2} = {( - 7 - 7)^2} + {(1 + 1)^2}$
On simplifying we get,
$ \Rightarrow B{C^2} = 196 + 4$
$ \Rightarrow B{C^2} = 200$
Again using the distance formula on A(-5,5) and C(7,-1), we get,
$i.e.,C{A^2} = {(7 + 5)^2} + {( - 1 - 5)^2}$
On simplifying we get,
$ \Rightarrow C{A^2} = 144 + 36$
$ \Rightarrow C{A^2} = 180$
In triangle QPR if right-angled at P,
Then, $Q{R^2} = P{Q^2} + P{R^2}$ {known as Pythagoras theorem}
In triangle ABC, we can see that
$B{C^2} = A{B^2} + C{A^2}$
Therefore, A will be right-angled.
Therefore, A(-5, 5) will be the orthocenter of the triangle.
Option(C) is correct.
Note: In the above solution we said that the orthocenter of a right-angled triangle is the vertex with the right angle. Let us discuss that,
If we draw a perpendicular from either base or altitude of the right-angled triangle to a side other than hypotenuse, it will come out to be the vertex with the right angle and is the same for the other side.
Since the outcome will remain the same as the vertex will the intersection point of the base’s perpendicular line i.e. altitude and vice versa. So we conclude that the vertex with the right angle in the right-angled triangle is also the orthocenter of the triangle.
Once we get the sides of the triangle, we try to find if the triangle is an equilateral or right-angled triangle for the easy approach for the solution.
Complete step-by-step answer:
Given data: Mid-points of the sides of the triangle as \[\left( {0,{\text{ }}0} \right),{\text{ }}\left( {1,{\text{ }}2} \right)\] and \[\left( { - 6,{\text{ }}3} \right)\]

Let the triangle be ABC with the vertices as A(a, b), B(p, q), and C(l,m), i.e.

If the point (x, y) is the midpoint of $\left( {{x_1},{y_1}} \right)$and $\left( {{x_2},{y_2}} \right)$
Then, $x = \dfrac{{{x_1} + {x_2}}}{2}$
And $y = \dfrac{{{y_1} + {y_2}}}{2}$
Using this midpoint formula on side BC,
$ \Rightarrow \dfrac{{p + l}}{2} = 0$
$ \Rightarrow p = - l$,
and $\dfrac{{q + m}}{2} = 0$
$ \Rightarrow q = - m$
Using the midpoint formula on side AB,
$ \Rightarrow \dfrac{{a + p}}{2} = - 6$
$ \Rightarrow a + p = - 12...............(i),$
And $\dfrac{{b + q}}{2} = 3$
$ \Rightarrow b + q = 6................(ii)$
Using the midpoint formula on side CA,
$ \Rightarrow \dfrac{{l + a}}{2} = 1$
$ \Rightarrow l + a = 2................(iii)$,
And $\dfrac{{m + b}}{2} = 2$
$ \Rightarrow m + b = 4....................(iv)$
Substituting the value of ‘p’ in equation(i)
i.e.$a - l = - 12............(v)$
Substituting the value of ‘q’ in equation(ii)
i.e.$b - m = 6............(vi)$
now adding equation(iii) and (v)
i.e. $2a = - 10$
$\therefore a = - 5$
Substituting $a = - 5$in equation(v)
i.e., $l = 12 - 5$
$\therefore l = 7$
Since, $p = - l$
$\therefore p = - 7$
now adding equation(iv) and (vi)
i.e. $2b = 10$
$\therefore b = 5$
Substituting $b = 5$in equation(vi)
i.e., $m = 5 - 6$
$\therefore m = - 1$
Since, $q = - m$
$\therefore q = 1$
From the values of a,b,p,q,l,m we can say that the vertices of triangle ABC are
A(-5,5), B(-7,1), and C(7,-1)
Distance between two points U$\left( {{x_1},{y_1}} \right)$and V$\left( {{x_2},{y_2}} \right)$ is given by
$UV = \sqrt {{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2}} $
$ \Rightarrow U{V^2} = {({x_1} - {x_2})^2} + {({y_1} - {y_2})^2}$
On substituting values of A(-5,5) and B(-7,1), we get
$\therefore A{B^2} = {( - 5 + 7)^2} + {(5 - 1)^2}$
On simplifying we get,
$ \Rightarrow A{B^2} = 4 + 16$
$ \Rightarrow A{B^2} = 20$
Again using the distance formula on B(-7,1), and C(7,-1)
$i.e.,B{C^2} = {( - 7 - 7)^2} + {(1 + 1)^2}$
On simplifying we get,
$ \Rightarrow B{C^2} = 196 + 4$
$ \Rightarrow B{C^2} = 200$
Again using the distance formula on A(-5,5) and C(7,-1), we get,
$i.e.,C{A^2} = {(7 + 5)^2} + {( - 1 - 5)^2}$
On simplifying we get,
$ \Rightarrow C{A^2} = 144 + 36$
$ \Rightarrow C{A^2} = 180$
In triangle QPR if right-angled at P,
Then, $Q{R^2} = P{Q^2} + P{R^2}$ {known as Pythagoras theorem}
In triangle ABC, we can see that
$B{C^2} = A{B^2} + C{A^2}$
Therefore, A will be right-angled.
Therefore, A(-5, 5) will be the orthocenter of the triangle.
Option(C) is correct.
Note: In the above solution we said that the orthocenter of a right-angled triangle is the vertex with the right angle. Let us discuss that,
If we draw a perpendicular from either base or altitude of the right-angled triangle to a side other than hypotenuse, it will come out to be the vertex with the right angle and is the same for the other side.
Since the outcome will remain the same as the vertex will the intersection point of the base’s perpendicular line i.e. altitude and vice versa. So we conclude that the vertex with the right angle in the right-angled triangle is also the orthocenter of the triangle.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




