
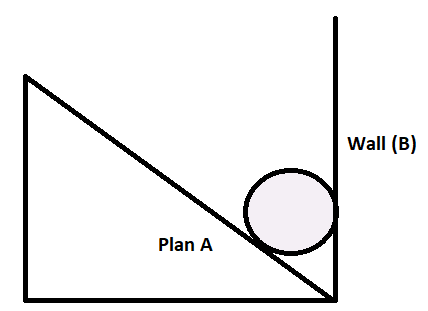
What will be the contact forces at A and B if the 50kg homogeneous smooth sphere rests on the incline A and bears the smooth vertical wall B?

Answer
547.5k+ views
Hint: This problem can be solved by using Lami's theorem. This theorem relates the magnitudes of the coplanar, concurrent and non – collinear forces that maintain an object in static equilibrium. This theorem can be used to analyze mechanical and structural systems.
Complete Step by Step Solution
The statement of Lami’s theorem is –
“When 3 forces performing at a point are in equilibrium, then every force is proportional to the sin of the angle between the opposite 2 forces”.
Lami’s theorem relates the magnitudes of coplanar, synchronal associated non-collinear forces that maintain an object in static equilibrium. The theory is incredibly helpful in analysing most of the mechanical moreover as structural systems.
In mathematics, this theorem can be represented as –
$ \dfrac{A}{{\sin \alpha }} = \dfrac{B}{{\sin \beta }} = \dfrac{C}{{\sin \gamma }} $
We have to use Lami's theorem in order to solve the question.
According to the question, it is given that, 50 kg homogeneous smooth sphere rests on the incline A and bears the smooth vertical wall B.
Therefore, by using the Lami’s theorem, we get –
$ \Rightarrow \dfrac{{mg}}{{\sin {{120}^ \circ }}} = \dfrac{{{R_1}}}{{\sin \left( {{{90}^ \circ } + {{60}^ \circ }} \right)}} = \dfrac{{{R_2}}}{{\sin {{90}^ \circ }}} $
Putting the value $ m = 50kg $ and $ g = 10 $ in the above equation, we get –
$ \Rightarrow \dfrac{{50 \times 10}}{{\sin \left( {{{90}^ \circ } + {{30}^ \circ }} \right)}} = \dfrac{{{R_1}}}{{\cos {{60}^ \circ }}} = \dfrac{{{R_2}}}{{{1^ \circ }}} $
From above equation, we can write it as –
$
\Rightarrow \dfrac{{500}}{{\sin \left( {{{90}^ \circ } + {{30}^ \circ }} \right)}} = {R_2} \\
\Rightarrow {R_2} = \dfrac{{500}}{{\sin \left( {{{120}^ \circ }} \right)}} \\
\Rightarrow {R_2} = \dfrac{{1000}}{{\sqrt 3 }}N \\
$
Using the value of $ {R_2} $ for finding the value of $ {R_1} $ , we get –
$ \Rightarrow {R_1} = \dfrac{{500}}{{\sqrt 3 }}N $
Hence, we got the contact forces at A and B as $ \dfrac{{500}}{{\sqrt 3 }}N $ and $ \dfrac{{1000}}{{\sqrt 3 }}N $ .
Note:
Students often make mistakes while taking angle between components of force. It must be remembered that normal always acts as perpendicular to the surface and point of contact. Therefore, in the case of a sphere, it always passes from the center.
Complete Step by Step Solution
The statement of Lami’s theorem is –
“When 3 forces performing at a point are in equilibrium, then every force is proportional to the sin of the angle between the opposite 2 forces”.
Lami’s theorem relates the magnitudes of coplanar, synchronal associated non-collinear forces that maintain an object in static equilibrium. The theory is incredibly helpful in analysing most of the mechanical moreover as structural systems.
In mathematics, this theorem can be represented as –
$ \dfrac{A}{{\sin \alpha }} = \dfrac{B}{{\sin \beta }} = \dfrac{C}{{\sin \gamma }} $
We have to use Lami's theorem in order to solve the question.
According to the question, it is given that, 50 kg homogeneous smooth sphere rests on the incline A and bears the smooth vertical wall B.
Therefore, by using the Lami’s theorem, we get –
$ \Rightarrow \dfrac{{mg}}{{\sin {{120}^ \circ }}} = \dfrac{{{R_1}}}{{\sin \left( {{{90}^ \circ } + {{60}^ \circ }} \right)}} = \dfrac{{{R_2}}}{{\sin {{90}^ \circ }}} $
Putting the value $ m = 50kg $ and $ g = 10 $ in the above equation, we get –
$ \Rightarrow \dfrac{{50 \times 10}}{{\sin \left( {{{90}^ \circ } + {{30}^ \circ }} \right)}} = \dfrac{{{R_1}}}{{\cos {{60}^ \circ }}} = \dfrac{{{R_2}}}{{{1^ \circ }}} $
From above equation, we can write it as –
$
\Rightarrow \dfrac{{500}}{{\sin \left( {{{90}^ \circ } + {{30}^ \circ }} \right)}} = {R_2} \\
\Rightarrow {R_2} = \dfrac{{500}}{{\sin \left( {{{120}^ \circ }} \right)}} \\
\Rightarrow {R_2} = \dfrac{{1000}}{{\sqrt 3 }}N \\
$
Using the value of $ {R_2} $ for finding the value of $ {R_1} $ , we get –
$ \Rightarrow {R_1} = \dfrac{{500}}{{\sqrt 3 }}N $
Hence, we got the contact forces at A and B as $ \dfrac{{500}}{{\sqrt 3 }}N $ and $ \dfrac{{1000}}{{\sqrt 3 }}N $ .
Note:
Students often make mistakes while taking angle between components of force. It must be remembered that normal always acts as perpendicular to the surface and point of contact. Therefore, in the case of a sphere, it always passes from the center.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light




