Question

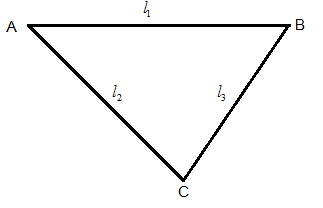
The compensated pendulum of a clock consists of an isosceles triangular frame of base length \[{l_1}\] and expansivity \[{\alpha _1}\] and slides of length \[{l_2}\] and expansivity \[{\alpha _2}\]. The pendulum is supported, as shown in Figure. Find the ratio \[\dfrac{{{l_1}}}{{{l_2}}}\] so that the length of the pendulum may remain unchanged at all temperatures.

A. \[\dfrac{{{l_1}}}{{{l_2}}} = 2\sqrt {\dfrac{{{a_2}}}{{{a_1}}}} \]
B. \[\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{{{a_2}}}{{{a_1}}}\]
C. \[\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{{{a_2}}}{{2{a_1}}}\]
D. \[\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{{2{a_2}}}{{{a_1}}}\]

Answer 1

Hint: Three basic thermal expansions are linear expansion, superficial expansion and cubical expansion. Here, in the question we need to determine the ratio \[\dfrac{{{l_1}}}{{{l_2}}}\] so that the length of the pendulum may remain unchanged at all temperatures. For this the amount a material expands or contracts per unit length due to a one-degree change in temperature.

Complete step by step answer:
Let C be the base of the triangle,
Now draw a perpendicular bisector on the side AB from the vertex C

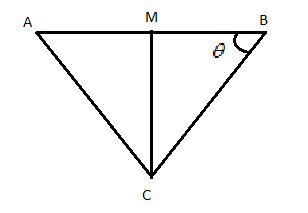
Here \[\cos \theta = \dfrac{{BM}}{{BC}} = \dfrac{{\dfrac{1}{2}BM}}{{BC}} = \dfrac{{{l_1}}}{{2{l_2}}}\]
Now when the triangle expands,
Let A’B’C be the new triangle and draw a perpendicular AN from A to A’C

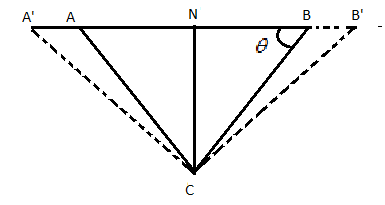
Here AA’=x increase in the length of AB\[ = \dfrac{1}{2}{l_1}{\alpha _1}t\], where t is the increase in temperature and
A’N= increase in the length of AB\[ = {l_2}{\alpha _2}t\]
Since the change in angle after the expansion is very small, hence we can write
\[\angle BAC = \angle B'A'C = \theta \]
Hence
\[\cos \theta = \dfrac{{A'N}}{{AA'}} - - (i)\]
Where \[\cos \theta = \dfrac{{{l_1}}}{{2{l_2}}}\]
Hence substituting the value in equation (i), we get
\[\dfrac{{{l_1}}}{{2{l_2}}} = \dfrac{{{l_2}{\alpha _2}t}}{{\dfrac{1}{2}{l_1}{\alpha _1}t}}\]
By solving
\[
  \dfrac{{{l_1}}}{{2{l_2}}} = \dfrac{{2{l_2}{\alpha _2}}}{{{l_1}{\alpha _1}}} \\
  {\left( {\dfrac{{{l_1}}}{{{l_2}}}} \right)^2} = 4\dfrac{{{\alpha _2}}}{{{\alpha _1}}} \\
  \dfrac{{{l_1}}}{{{l_2}}} = \sqrt {4\dfrac{{{\alpha _2}}}{{{\alpha _1}}}} \\
   = 2\sqrt {\dfrac{{{\alpha _2}}}{{{\alpha _1}}}} \\
 \]
Hence the ratio \[\dfrac{{{l_1}}}{{{l_2}}}\]so that the length of the pendulum may remain unchanged at all temperatures \[ = 2\sqrt {\dfrac{{{\alpha _2}}}{{{\alpha _1}}}} \]

So, the correct answer is “Option A”.

Note:
Expansion corresponds to change in length, area and volume of the substance where linear expansivity is the increase in the length of a substance for per unit length of the substance for one degree Celsius rise in temperature.