Question

The circumcenter of the triangle with vertices \[(0,30)\] , \[(4,0)\] and \[(30,0)\] is
A.\[(10,10)\]
B.\[(10,12)\]
C.\[(12,12)\]
D.\[(15,15)\]
E.\[(17,17)\]

Answer 1

Hint: The circumcenter is the center point of the circumcircle drawn around a polygon. The circumcircle of a polygon is the circle that passes through all of its vertices and the center of that circle is called the circumcenter. All polygons that have a circumcircle are known as cyclic polygons. Only regular polygons, triangles, rectangles, and right-kites can have the circumcircle and thus the circumcenter.

Complete step-by-step answer:
Steps to construct the circumcenter of a triangle:
Step 1: Draw the perpendicular bisectors of all the sides of the triangle using a compass.
Step 2: Extend all the perpendicular bisectors to meet at a point. Mark the intersection point as O, this is the circumcenter.
Step 3: Using a compass and keeping O as the center and any vertex of the triangle as a point
on the circumference, draw a circle, this circle is our circumcircle whose center is O.

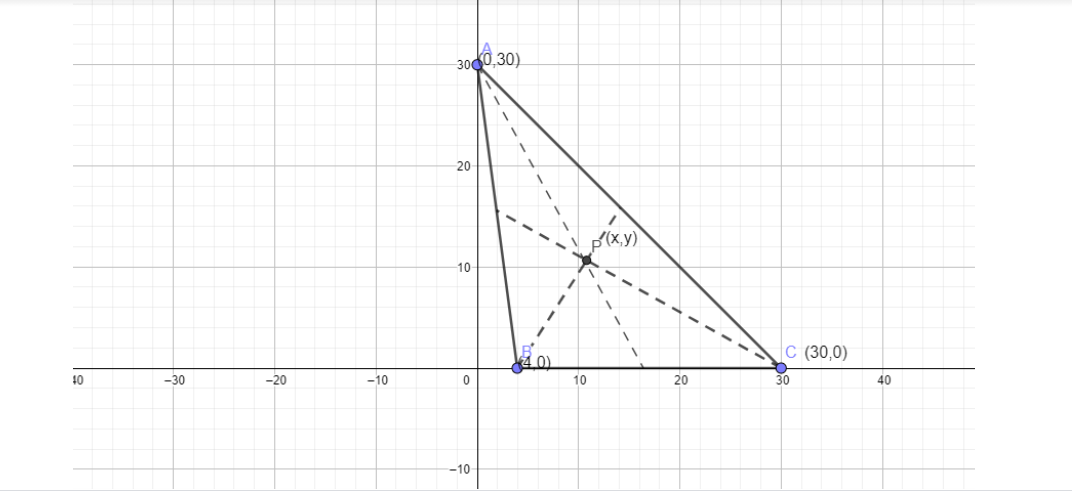
Assume that the circumcenter of a triangle is P(x,y)
The vertices are given to us as follows
A \[(0,30)\]
B \[(4,0)\]
C \[(30,0)\]
we have the following equations using the distance formula :
\[AP = \sqrt {{{(x - 0)}^2} + {{\left( {y - 30} \right)}^2}} \]
\[BP = \sqrt {{{(x - 4)}^2} + {{\left( {y - 0} \right)}^2}} \]
And
\[CP = \sqrt {{{(x - 30)}^2} + {{\left( {y - 0} \right)}^2}} \]
Since the vertices of the triangle are equidistant from the circumcenter .
Therefore we get
AP=BP=CP
Now using the first and second equality we have
\[\sqrt {{{(x - 0)}^2} + {{\left( {y - 30} \right)}^2}} \] = \[\sqrt {{{(x - 4)}^2} + {{\left( {y - 0} \right)}^2}} \]
Squaring both the sides we get
\[{(x - 0)^2} + {\left( {y - 30} \right)^2}\] = \[{(x - 4)^2} + {\left( {y - 0} \right)^2}\]
Which simplifies to
\[{x^2} + {y^2} + 900 - 60y = {x^2} + 16 - 8x + {y^2}\]
On further simplification we get
\[900 + 60y = 16 + 8x\]
On further simplification we get
\[221 = 15y - 2x\] …(1)
 Now using the second and third equality we get
\[\sqrt {{{(x - 4)}^2} + {{\left( {y - 0} \right)}^2}} = \sqrt {{{(x - 30)}^2} + {{\left( {y - 0} \right)}^2}} \]
Squaring both the sides we get
\[{(x - 4)^2} + {\left( {y - 0} \right)^2} = {(x - 30)^2} + {\left( {y - 0} \right)^2}\]
Which simplifies to
\[{x^2} + 16 - 8x + {y^2} = {x^2} + 900 - 60x + {y^2}\]
On further simplification we get
\[884 = 52x\]
Therefore we get
\[x = 17\]
Now putting this value of \[x\] in (1) we get
\[y = 17\]
Therefore the point of circumcentre \[(17,17)\]
Therefore option (E) is the correct answer.
So, the correct answer is “Option E”.

Note: Properties of circumcenter are: Consider any triangle ABC with circumcenter O.
A) All the vertices of the triangle are equidistant from the circumcenter.
B) All the new triangles formed by joining O to the vertices are Isosceles triangles.