
The circuit is equivalent to
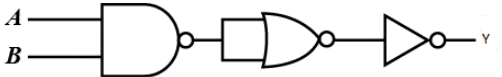
(A) NOR gate
(B) AND gate
(C) NAND gate
(D) OR gate
Answer
581.1k+ views
Hint:Here we correctly deduce the type of gate and then keep on finding the output of gate after another. The output of one gate is the input of the other gate.
Complete step by step answer:
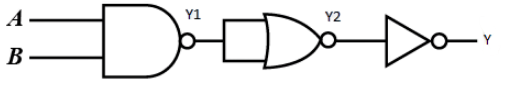
The inputs are A and B.
They are NAND gate inputs.
Let ${Y_1}$ be the first input and ${Y_2}$ be the second input.
So,${Y_1} = \overline {A.B} $
${Y_1}$ is input to NOR gate.
So, output of ${Y_2} = \overline {\left( {\overline {A.B} } \right)} = A.B$
${Y_2}$ is input to NOT gate-
So, output of $Y = \overline {A.B} $
The output of the circuit is NAND gate.Therefore, option C is correct.
Additional information:
First let us see what an AND gate is and how it is represented-
The AND gate is so named because the gate behaves in the same manner as the logical “and” operator, whether $0$ is considered “false” and $1$ is considered true. The output is “true” because the inputs are also “true”.
Now let us see what OR gate is and its truth table:The OR gate drives its name from the fact that it operates according to the logical inclusive or mode. Whether one or all of the inputs are real, the output is true. If all inputs are false, the output is false. In other words, for the output to be $1$ at least one of the two inputs must be $1$
Note:Here we may get confused as to which gate will NOR and which will be NAND but we have to remember how NAND and NOR gates are represented otherwise we shall get a different answer.
Complete step by step answer:
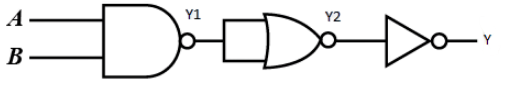
The inputs are A and B.
They are NAND gate inputs.
Let ${Y_1}$ be the first input and ${Y_2}$ be the second input.
So,${Y_1} = \overline {A.B} $
${Y_1}$ is input to NOR gate.
So, output of ${Y_2} = \overline {\left( {\overline {A.B} } \right)} = A.B$
${Y_2}$ is input to NOT gate-
So, output of $Y = \overline {A.B} $
The output of the circuit is NAND gate.Therefore, option C is correct.
Additional information:
First let us see what an AND gate is and how it is represented-
The AND gate is so named because the gate behaves in the same manner as the logical “and” operator, whether $0$ is considered “false” and $1$ is considered true. The output is “true” because the inputs are also “true”.
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Now let us see what OR gate is and its truth table:The OR gate drives its name from the fact that it operates according to the logical inclusive or mode. Whether one or all of the inputs are real, the output is true. If all inputs are false, the output is false. In other words, for the output to be $1$ at least one of the two inputs must be $1$
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Note:Here we may get confused as to which gate will NOR and which will be NAND but we have to remember how NAND and NOR gates are represented otherwise we shall get a different answer.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




