Question

The circle $ {{x}^{2}}+{{y}^{2}}-2x-2y+1=0 $ is rolled along the positive direction of the x-axis and makes one complete roll. Find its equation in a new position.

Answer 1

Hint: To find out the new equation of circle we will found the ne coordinates of centre of circle, through distance method, and the radius of circle will remain unchanged so by using the new coordinates and radius of circle we will found out the equation of circle in new position.

Complete step by step answer:
As we know that standard form of equation of circle is${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$in which$(-g,-f)$are the coordinates of centre i.e. (x, y) and radius is$\sqrt{{{g}^{2}}+{{f}^{2}}-c}$. So comparing this standard form with the equation${{x}^{2}}+{{y}^{2}}-2x-2y+1=0$, -g is 1, -f is 1 and radius is$\sqrt{{{1}^{2}}+{{1}^{2}}-1}=1$also 1.

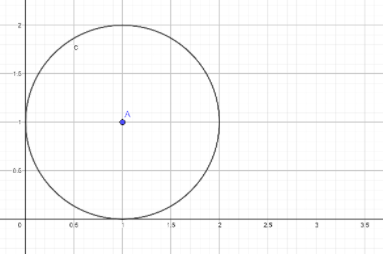
So we got the circle as represented in the figure, whose centre is$(1,1)$denoted by ‘A’ and radius is also 1. Now according to the question circle moved to the positive x-axis to one complete roll of itself. That means we can say that a circle has moved the distance equal to its circumference, as circumference is the value that measures the length of roll of circle.
So to complete one complete roll circle had moved the distance equal to its circumference. As we know that the circumference of a circle is$=2\pi r$where r is the radius of the circle which is unit 1 in our case. So circumference of circle will be;
$\begin{align}
  & =2\pi r \\
 & =2\times \dfrac{22}{7}\times 1 \\
 & =\dfrac{44}{7} \\
\end{align}$
So the circle had moved$\dfrac{44}{7}$ unit in the positive x-axis. As the circle had moved with it, all the points lying on it had also moved the same distance, so we can say that the centre of the circle had also travelled the same distance in positive x-axis. Since it is moving only in x-axis, the y coordinate will remain the same for it, when it has completed its one complete roll. So we can say that the x coordinate of the centre of the circle had travelled$\dfrac{44}{7}$ unit in the positive x-axis from the initial point. So by distance formula we know that distance between two points is$\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$in which$({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})$ are the coordinates of point, and in our case they are coordinate of centre. So$({{x}_{1}},{{y}_{1}})$will be$(1,1)$and$({{x}_{2}},{{y}_{2}})$we had to find. Whose distance is$\dfrac{44}{7}$.
So$({{x}_{2}},{{y}_{2}})$will be;
\[\begin{align}
  & \dfrac{44}{7}=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}} \\
 & \dfrac{44}{7}=\sqrt{{{({{x}_{2}}-1)}^{2}}+{{({{y}_{2}}-1)}^{2}}} \\
\end{align}\]
Since there is no movement in y-axis so y coordinate of centre will remain same after complete of one roll so${{y}_{2}}$will be 1 which is initial y coordinate of centre. So we will get;
\[\begin{align}
  & \dfrac{44}{7}=\sqrt{{{({{x}_{2}}-1)}^{2}}+{{(1-1)}^{2}}} \\
 & \dfrac{44}{7}=\sqrt{{{({{x}_{2}}-1)}^{2}}} \\
 & \dfrac{44}{7}=({{x}_{2}}-1) \\
 & \dfrac{51}{7}={{x}_{2}} \\
\end{align}\]

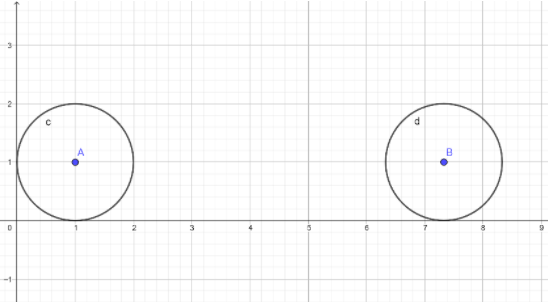
So new coordinate of centre is$({{x}_{2}},{{y}_{2}})$i.e.$\left( \dfrac{51}{7},1 \right)$, as represented in figure market as B
So equation of circle at new position will be; ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ in which$(-g,-f)$are the coordinates of centre i.e.$({{x}_{2}},{{y}_{2}})$and radius is$\sqrt{{{g}^{2}}+{{f}^{2}}-c}$. So by comparing it we will get equation of circle at new position is;
\[\begin{align}
  & {{x}^{2}}+{{y}^{2}}+2\left( -\dfrac{51}{7} \right)x+2(-1)y+c=0 \\
 & {{x}^{2}}+{{y}^{2}}-\dfrac{102}{7}x-2y+c=0 \\
\end{align}\]
As radius is equal to 1, and according to standard form of circle it is$\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
So, by simplifying it we will get;
 $\begin{align}
  & r=\sqrt{{{g}^{2}}+{{f}^{2}}-c} \\
 & 1=\sqrt{{{\left( \dfrac{51}{7} \right)}^{2}}+{{1}^{2}}-c} \\
 & {{1}^{2}}={{\left( \dfrac{51}{7} \right)}^{2}}+{{1}^{2}}-c \\
 & c={{\left( \dfrac{51}{7} \right)}^{2}} \\
\end{align}$
So the equation of circle will be;
Hence the answer is\[{{x}^{2}}+{{y}^{2}}-\left( \dfrac{102}{7} \right)x-2y+{{\left( \dfrac{51}{7} \right)}^{2}}=0\]i.e. equation of circle in new position is\[{{x}^{2}}+{{y}^{2}}-\left( \dfrac{102}{7} \right)x-2y+{{\left( \dfrac{51}{7} \right)}^{2}}=0\].

Note: Other than this we can write the equation of circle in new position as $ {{\left( x-\dfrac{37}{4} \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1 $ which is in the form of $ {{\left( x-g \right)}^{2}}+{{\left( y-f \right)}^{2}}={{r}^{2}} $ in which $ (-g,-f) $ are the coordinates of centre and ‘r’ is the radius of circle. Both answer are correct i.e. $ {{\left( x-\dfrac{37}{4} \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1 $ and\[{{x}^{2}}+{{y}^{2}}-\dfrac{37}{2}x-2y+\dfrac{37}{4}=0\].