Question

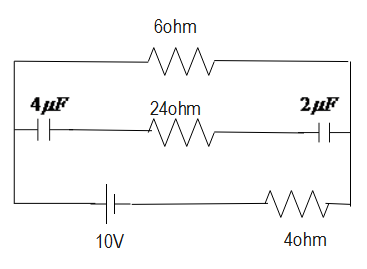
: The charge developed on $4\mu F$ condenser is:

Answer 1

Hint: In this question, we will use the relation between the charge, capacitance and voltage. Also, by substituting the given values we will get the required result. Further, we will study the basics of a simple electric circuit.
Formula used:
$Q = CV$

Complete answer:
We know that the electrical charge of a circuit or device is defined as the capacitance times the voltage of a given circuit.
We know, from the ohm’s law:
$I = \dfrac{V}{R}$
By putting the values in above equation, we get:
$I = 1A$
Potential difference developed across $4\mu F$ condenser in the circuit:
$P.D = 2.5 - (0.5 \times 1)$
$ \Rightarrow P.D = 2V$
Now, the charge developed is given by:
$Q = CV$
Now, by substituting the values in the above equation, we get:
$\eqalign{& Q = 4 \times 2 \cr
  & \therefore Q = 8\mu C \cr} $
Therefore, we get the required result, which tells us the charge developed on the given condenser.

Additional information:
We should know that in a series circuit, the output current of the first resistor flows into the input of the second resistor; so, the current is the same in each resistor whereas In a parallel circuit, all of the resistor are on connected together on one side and all the leads on the other side are connected together.
In a circuit if the resistance is constant over a range of voltage, then I = V/R, can be used to predict the behavior of the material. This involves DC current and voltage, it is the same for the resistors. Further, a material obeys Ohm's law or does not obey; the resistance of the material can be described in terms of its bulk. The resistivity, and the resistance both, is temperature dependent. Over certain ranges of temperature, this temperature dependence can be predicted from resistance.

Note:
In series connection the resistances are directly added whereas in parallel connection resistance is added inversely. Internal resistance of a circuit refers to the opposition to the flow of current offered by the cells and batteries themselves thereby, resulting in the generation of heat. Internal resistance and resistance both are measured in Ohms.