Question

The centres of two identical small conducting spheres are 1m apart. They carry charges of opposite kinds and attract each other with a force F. When they are connected by a conducting thin wire they repel each other with a force $\dfrac{F}{3}$. What is the ratio of magnitude of charges carried by the spheres initially?
A. 1:1
B. 2:1
C. 3:1
D. 4:1

Answer 1

Hint: Using Coulomb’s law for electric force, determine the expression for the attractive force between the two spheres in the first case by assuming the charges they carry to be $q_1$ and $q_2$ respectively, keeping in mind that they are oppositely charged. Then, recall that when the spheres are connected by a thin conducting wire, there is a flow of charge due to a potential difference between them, directed from the positively charged to the negatively charged region.
This stops only after both the spheres have obtained an equal magnitude of charge, which causes them to repel with the force as given in the equation. Obtain the relation for this force and evaluate the resulting equation to obtain the required ratio.

Formula used:
Electric force between two charges: $F = \dfrac{1}{4\pi\epsilon}\dfrac{q_1 q_2}{r^2}$

Complete step-by-step answer:
From Coulomb’s law, we know that the force experienced by two charges $q_1$ and $q_2$ placed at a distance r from each other in free space can be given as:
$F = \dfrac{kq_1 q_2}{r^2}$, where $k = \dfrac{1}{4\pi\epsilon_0}$, where $\epsilon_0$ is the electrical permittivity of free space.
Let us consider the first case, when the two spheres experience an attractive force with respect to each other.

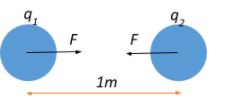
Since they carry opposite charges, let the charges on the spheres be $q_1$ and $q_2$ respectively. Given that they are identical spheres, they both experience the same force of attraction that is directed towards each other, and is given by Coulomb’s law:
$F = \dfrac{kq_1(q_2)}{1^2} = kq_1 q_2$
Now, when the two spheres are connected by a conducting wire, charge begins to flow from one conductor to the other from higher potential (dominantly positively charged conductor) to lower potential (dominantly negatively charged conductor). This flow of charge continues until both the spheres attain the same potential when there is no longer a potential difference between them.

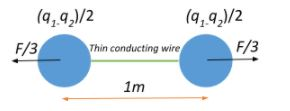
In this case, the charges on both the spheres will be the same, and will be an equivalent distribution of the potential difference ($q_1-q_2$) between them. Let the charge on each of the spheres in this case be $\dfrac{q_1-q_2}{2}$.
Since they are like charged, they repel each other with a force given as:
$F^{\prime} = \dfrac{k\left(\dfrac{q_1-q_2}{2}\right). \left(\dfrac{q_1-q_2}{2}\right)}{1^2} = k\left(\dfrac{q_1-q_2}{2}\right). \left(\dfrac{q_1-q_2}{2}\right)$
But we are given that $F^{\prime} = \dfrac{F}{3}$
$\Rightarrow \dfrac{F}{3} = k\left(\dfrac{q_1-q_2}{2}\right). \left(\dfrac{q_1-q_2}{2}\right)$
$\Rightarrow \dfrac{ kq_1 q_2}{3} = \dfrac{k}{4}\left(q_1^2 -q_1q_2-q_2q_1+q_2^2\right)$
$\Rightarrow 4q_1q_2 = 3q_1^2 -6q_1q_2+3q_2^2$
$\Rightarrow 3q_1^1 -10q_1q_2+3q_2^2=0$
Solving the above equation quadratically:
$\Rightarrow 3q_1^2 -9q_1q_2 – q_1q_2 +3q_2^2 = 0$
$\Rightarrow 3q_1(q_1-3q_2) – q_2(q_1-3q_2)=0$
$\Rightarrow (3q_1-q_2).(q_1-3q_2)=0$
Taking $(q_1-3q_2)=0$
$\Rightarrow q_1 = 3q_2$
$\Rightarrow \dfrac{q_1}{q_2} = \dfrac{3}{1}$
$\Rightarrow q_1:q_2 = 3:1$
Therefore, the correct choice is: C. 3:1

So, the correct answer is “Option C”.

Note: Remember that when the two spheres are connected by the conducting wire, there is always a flow of charge if there exists a potential difference between them such that charges flow from a high potential to a low potential, synonymous to the flow of charge from the positive terminal to the negative terminal of a battery in a circuit since a potential difference sets up an electric field.
Also do not forget that for spherical conductors, charges distribute themselves on the outermost surface so that conducting wire provides only a path for charge transfer and no charge resides on the wire. This is because charges always reside in a way to minimize the potential energy of the system by making the surface an equipotential surface.