Question

The capacity of an isolated sphere is increased $n$ times when it is enclosed by an earthed concentric sphere. The ratio of their radii is
(A) $\dfrac{n}{n-1}$
(B) $\dfrac{{{n}^{2}}}{n-1}$
(C) $\dfrac{2n}{n+1}$
(D) $\dfrac{2n+1}{n+1}$

Answer 1

Hint : To solve this question we have to find the capacitance of two spheres both is concentric. After finding capacitance we have compared both of the equations to find the ratio of their radius.

Complete step by step answer: Let the radius of a first sphere is ${{R}_{1}}$ and radius of other sphere is ${{R}_{2}}$

Here is the potential on the surface of a sphere is \[V=\dfrac{KQ}{{{R}_{1}}}\]
We let the second plate on the infinite and potential so \[{{V}_{1}}=0\]
Now we calculate the potential difference between the surface of the sphere and plate on the infinite. Let the difference between both refer to \[\Delta V\].
So we can write the equation as
 \[\Delta V=V-{{V}_{1}}\]
Here we put the values in the equation
 \[\Delta V=\dfrac{KQ}{{{R}_{1}}}-0\]
Then we get,
 \[\Delta V=\dfrac{KQ}{{{R}_{1}}}\]
Now we put the value of\[K\]in the above equation
 \[K=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\]
After putting the value of K we get,
 \[\Delta V=\dfrac{1}{4\pi {{\varepsilon }_{0}}{{R}_{1}}}\cdot Q\]

Now we calculate charge in the sphere using the following equation
 \[Q=C\Delta V\]
Here we put the value of the potential difference in the above equation
 \[Q={{C}_{1}}\cdot \dfrac{Q}{4\pi {{\varepsilon }_{0}}{{R}_{1}}}\]
After solving this equation we get
 \[{{C}_{1}}=4\pi {{\varepsilon }_{0}}{{R}_{1}}\]
Here we get the capacitance in the first sphere.
Now we calculate capacitance on the outer sphere.

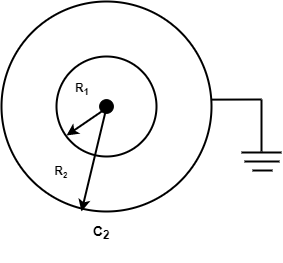
The charge on the outer surface of the sphere is negative. And in the inner sphere charge is positive.
So we calculate total potential by both spheres,
 $V=\dfrac{-KQ}{{{R}_{2}}}$
 ${{V}_{1}}=\dfrac{KQ}{{{R}_{2}}}$
So the total potential of both sphere is
 \[\Delta V=\dfrac{-KQ}{{{R}_{2}}}+\dfrac{KQ}{{{R}_{1}}}\]
Now take K as a common value in the equation
 \[\Delta V=K\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]
Now we put the value of \[K\] in the above equation,
 $\Delta V=\dfrac{Q}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
Here we calculate charge in the sphere,
 $Q={{C}_{2}}\Delta V$
Here we put the value of the total potential in both sphere,
 $Q={{C}_{2}}\cdot \dfrac{Q}{4\pi {{\varepsilon }_{0}}}\left( \dfrac{{{R}_{2}}-{{R}_{1}}}{{{R}_{1}}{{R}_{2}}} \right)$
After solving this equation we get the capacitance of both spheres,
 ${{C}_{2}}=\dfrac{4\pi {{\varepsilon }_{0}}{{R}_{1}}{{R}_{2}}}{{{R}_{2}}-{{R}_{1}}}$
As mentioned in the question the value capacitance of ${{C}_{2}}$ change in $n$ times of ${{C}_{1}}$
 $n{{C}_{1}}=n\cdot 4\pi {{\varepsilon }_{0}}{{R}_{1}}$
Now comparing both equations,
 ${{C}_{2}}=\dfrac{4\pi {{\varepsilon }_{0}}{{R}_{1}}{{R}_{2}}}{{{R}_{2}}-{{R}_{1}}}=n{{C}_{1}}=n\cdot 4\pi {{\varepsilon }_{0}}{{R}_{1}}$
After solving this equation we get,
 \[\Rightarrow \dfrac{{{R}_{2}}}{{{R}_{2}}-{{R}_{1}}}=n\]
After solving this we get,
 \[\Rightarrow {{R}_{2}}=n{{R}_{2}}-n{{R}_{1}}\]
Take \[{{R}_{2}}\] in the other side so we can take \[{{R}_{2}}\] it as a common term
 \[n{{R}_{1}}=n{{R}_{2}}-{{R}_{2}}\]
After taking \[{{R}_{2}}\] we get
\[n{{R}_{1}}=(n-1){{R}_{2}}\]
After further solving
 \[\dfrac{{{R}_{2}}}{{{R}_{1}}}=\dfrac{n}{n-1}\]
Here we get the ratio between both spheres is \[=\dfrac{n}{n-1}\]

Note: To solve this type of question we have to find the potential difference of both spheres. After that, we calculate charge in both spheres. The charge of the outer sphere is negative but the charge of the inner sphere is positive. Then we calculate the capacitance of both spheres then compares both of them to calculate the ratio of the radius. If we follow these steps we can easily solve this question.