Question

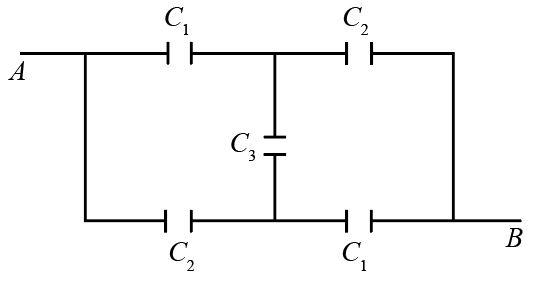
The capacity between the point A and B in the adjoining circuit will be

A. $\dfrac{{2{C_1}{C_2} + {C_3}\left( {{C_1} + {C_2}} \right)}}{{{C_1} + {C_2} + 2{C_3}}}$
B.$\dfrac{{{C_1}{C_2} + {C_2}{C_3} + {C_3}{C_1}}}{{{C_1} + {C_2} + {C_3}}}$
C.$\dfrac{{{C_1}\left( {{C_2} + {C_3}} \right) + {C_2}\left( {{C_1} + {C_3}} \right)}}{{{C_1} + {C_2} + 3{C_3}}}$
D.\[\dfrac{{{C_1}{C_2}{C_3}}}{{{C_1}{C_2} + {C_2}{C_3} + {C_3}{C_1}}}\]

Answer 1

Hint: In this question, we will assume the total charge flowing in the circuit. We assume that a part of this charge will flow through a capacitor, and another part of this total charge will pass through another capacitor. The total charge in the circuit can be expressed as the product of voltage and the equivalent capacitance. This equivalent capacitance has the capacitance, which is equal to the sum of capacitance in the different capacitors. Then we will apply junction law, which says that the sum of all the incoming voltage at the terminal must be equal to the outgoing voltage. After solving the equation for the charges in capacitors, we will compare the equations formed, and then we will find the desired capacitance from terminal A and B.

Complete step by step answer:
The following is the schematic diagram of the circuit.

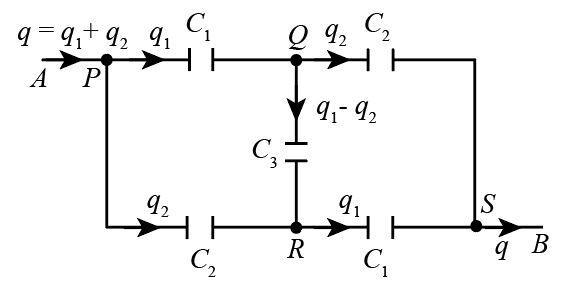
We will assume $q$ charge is flowing from the terminal $A$. Further ${q_1}$ part of charge $q$ will flow through capacitor ${C_1}$ and ${q_2}$ part of charge $q$ will flow through capacitor ${C_2}$. From terminal $Q$, ${q_1} - {q_2}$ will flow through ${C_3}$. Because of the symmetry$A$ ${q_1}$ charge will flow through another capacitor ${C_1}$ and ${q_2}$ charge will flow through another capacitor ${C_2}$. Assume voltage at terminal $P$ ,$Q$ ,$R$ and $S$ as ${V_P}$ ,${V_Q}$ ,${V_R}$ and ${V_s}$ respectively.

The total charge in the circuit can be expressed as:
$q = {C_{eq}}{V_P}$……(i)

Where, ${C_{eq}}$ is the equivalent capacitance in the circuit.

At terminal $Q$ , we will apply the junction law which can be expressed as:
$ {q_1} = {q_2} + {q_1} - {q_2}\\$
$ \implies \left( {{V_P} - {V_Q}} \right){C_1} = \left( {{V_Q} - 0} \right){C_2} + \left( {{V_Q} - {V_P} + {V_Q}} \right){C_3}\\ $
$\implies {V_P}{C_1} + {V_P}{C_2} = {V_Q}\left( {{C_1} + {C_2} + 2{C_3}} \right)\\$
$\implies {V_Q} = \dfrac{{{V_P}\left( {{C_1} + {C_3}} \right)}}{{{C_1} + {C_2} + 2{C_3}}}$..……(ii)
Now, we will find the charge ${q_1}$ in the circuit which can be expressed as:
${q_1} = \left( {{V_P} - {V_Q}} \right){C_1}$

In the above expression we will substitute the value of ${V_Q}$ from equation (ii), we get,
$ {q_1} = \left( {{V_P} - \dfrac{{{V_P}\left( {{C_1} + {C_3}} \right)}}{{{C_1} + {C_2} + 2{C_3}}}} \right){C_1}\\$
$\implies {q_1} = {C_1}{V_P}\left( {\dfrac{{{C_1} + {C_2} + 2{C_3} - {C_1} - {C_3}}}{{{C_1} + {C_2} + 2{C_3}}}} \right)\\$
$\implies {q_1} = {C_1}{V_P}\left( {\dfrac{{{C_2} + {C_3}}}{{{C_1} + {C_2} + 2{C_3}}}} \right)
……(iii) $

Similarly, we will find the charge ${q_2}$ in the circuit which can be expressed as:
${q_2} = {V_Q}{C_2}$

In the above expression we will substitute the value of ${V_Q}$ from equation (ii).
\[{q_2} = \dfrac{{{V_P}\left( {{C_1} + {C_3}} \right)}}{{{C_1} + {C_2} + 2{C_3}}}{C_2}\] ……(iv)

 Now, we will find the total charge $q$ by adding ${q_1}$ and${q_2}$ from equation (iii) and (iv)
$ q = {q_1} + {q_2}\\$
$ \implies q = {C_1}{V_P}\left( {\dfrac{{{C_2} + {C_3}}}{{{C_1} + {C_2} + 2{C_3}}}} \right) + {C_2}{V_P}\dfrac{{\left( {{C_1} + {C_3}} \right)}}{{{C_1} + {C_2} + 2{C_3}}}\\$
$ \implies q = {V_P}\dfrac{{{C_1}{C_2} + {C_1}{C_3} + {C_1}{C_2} + {C_2}{C_3}}}{{{C_1} + {C_2} + 2{C_3}}}\\ $
$\implies q = {V_P}\dfrac{{2{C_1}{C_2} + {C_3}\left( {{C_1} + {C_2}} \right)}}{{{C_1} + {C_2} + 2{C_3}}}$ ……(v)

But from equation (i) we know that $q = {C_{eq}}{V_P}$. On comparing equation (i) and (v) we get,
$q = {V_P}\dfrac{{2{C_1}{C_2} + {C_3}\left( {{C_1} + {C_2}} \right)}}{{{C_1} + {C_2} + 2{C_3}}} = {C_{eq}}{V_P}$

From the above comparison we have the value,
${C_{eq}} = \dfrac{{2{C_1}{C_2} + {C_3}\left( {{C_1} + {C_2}} \right)}}{{{C_1} + {C_2} + 2{C_3}}}$

So, the correct answer is “Option A”.

Note:
The charge that is flowing through the different capacitors is a part of total charge. We need to find the expression for the charges through different capacitors. We will always keep in mind that the capacitance offered by the capacitors separately will produce the same effect as equivalent capacitance.