Question

The capacitance between adjacent plates shown in the Fig is \[50nF\]. A $1\mu C$charge is placed on the middle plate. Find the charge on the outer surface of the upper plate and the potential difference between upper and middle plates:

(A) $0.5\mu C,10V$
(B) $1\mu C,20V$
(C) $0.5\mu C,20V$
(D) $1.0\mu C,40V$

Answer 1

Hint
When a charge $1\mu C$ is placed on the middle plate, a charge is formed on both the upper and lower surface of all the plates. Since the charge gets equally distributed, we can find the charge on the outer surface of the upper plate from there.
In this, we will use the formula,
${\text{Electric Field = }}\dfrac{{{Q_{total}}}}{{2S{\varepsilon _o}}}$
where ${Q_{total}}$ is the sum of all the charges, \[S\] is the surface area of the plates , ${\varepsilon _o}$ is permittivity in free space
and, \[V = \dfrac{Q}{C}\]
Where, $V$ is the potential difference, $Q$ is the charge on the plate, $C$ is the capacitance.

Complete Step by Step Solution

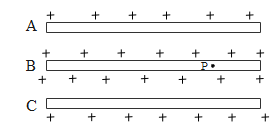
According to the problem, there are 3 parallel plates and the capacitance between them is given $50nF$. Now, we place a charge $1\mu C$ inside the middle plate.
On placing the charge $1\mu C$ at P, it spreads throughout the second plate and all of the plates acquire a positive charge on both its surfaces. The plate $A$ as a result acquires a negative charge on the lower surface and the plate $C$ acquires a negative charge on the upper surface. So, the outer surface of $A$ and the lower surface of $C$ acquires a positive charge.
The electric field is zero between the plates. Hence,
$\dfrac{{{Q_{tot}}}}{{2S{\varepsilon _o}}} = 0$
$ \Rightarrow \dfrac{1}{{2S{\varepsilon _o}}}\left[ {{q_A} - {q_A} + 1 - {q_B} - {q_B} + {q_C} - {q_C}} \right] = 0$
where ${q_A},{q_B}$ and ${q_C}$ are the charges on the upper and lower surfaces of plates $A,B$ and $C$ respectively.
So, from here by doing the calculation, we see that ${q_A}$ and ${q_C}$ both get cancelled.
$\therefore 2{q_B} = 1$
$ \Rightarrow {q_B} = 0.5C$
Thus, the charge on the upper surface of $B$ is
$1 - {q_B} = 0.5C$
The charge on the lower surface of $A$ is equal and opposite to that of the upper surface of $B$.
So,
 $ - {q_A} = - 0.5C$
From the figure, the upper surface of $A$ has a charge ${q_A} = 0.5C$.
To find the potential between the 2 plates, we use the formula, $V = \dfrac{{{q_A}}}{C}$.
So putting the values in the above equation, we get
$V = \dfrac{{0.5 \times {{10}^{ - 6}}}}{{50 \times {{10}^{ - 9}}}} = 10V$
Thus, the answer to the charge on the outer surface of the upper plate is $0.5\mu C$ and the potential between the upper and middle plate is 10V.
Correct option is (A).

Note
If the external charge had been negative, the charge would be negative on the plate $B$ and hence, the upper surface of the plate $A$ would have been different. So, we should be careful about the sign. But the value of the potential would have remained the same.