Question

The bulk modulus of rubber is \[9.8\times {{10}^{8}}{N}/{{{m}^{2}}}\;\]. To what height from the upper surface a rubber ball be taken in a lake so the volume of rubber ball decreased by\[0.1%\]?
(A) \[1m\]
(B) \[25m\]
(C) \[100m\]
(D) \[200m\]

Answer 1

Hint: In this question the volume strain (the decreased percentage of volume) is given and the bulk modulus is also given. The bulk modulus is the ratio of volume stress over volume strain and the actual volume stress is force per unit area but here the force per unit area is considered as pressure difference on the ball between the surface of the lake and the pressure at depth \[h\].
Formula used:
\[B=-\dfrac{\Delta P}{{}^{\Delta V}/{}_{V}}\]
 And \[P=\rho gh\].

Complete answer:
The bulk modulus of rubber is \[9.8\times {{10}^{8}}{N}/{{{m}^{2}}}\;\] is given.

The following figure indicates the ball at the surface of the lake. Assume at the surface of the lake, the volume and the pressure are \[V\]and \[{{P}_{0}}\] respectively.

When the ball taken in the lake with depth \[h\], assume the volume of the ball is \[V'\] and the pressure on the ball is \[P'\].The situation of the ball is given below,

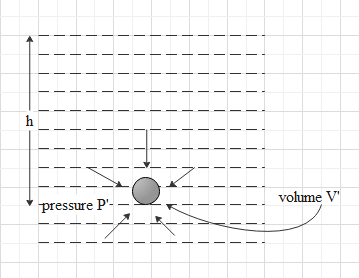
In the question the volume strain (the decreased percentage of volume) is given by \[0.1%\],
So, \[{}^{\Delta V}/{}_{V}\times 100=-0.1\]
So, \[{}^{\Delta V}/{}_{V}=-\dfrac{0.1}{100}=-{{10}^{-3}}\]
Here the negative sign denotes the decrease in volume.
Now bulk modulus \[B=9.8\times {{10}^{8}}{N}/{{{m}^{2}}}\;\] is given but the pressure at \[h\] depth is,
 So, \[P'={{P}_{0}}+\rho gh\]
So, \[\Delta P={{P}_{0}}-P'\]
\[\therefore \Delta P={{P}_{0}}-({{P}_{0}}-\rho gh)\]
\[\therefore \Delta P=\rho gh\]

Now applying the formula of bulk modulus,

\[B=-\dfrac{\Delta P}{{}^{\Delta V}/{}_{V}}\]
\[\therefore B=-\dfrac{\rho gh}{{}^{\Delta V}/{}_{V}}\]
\[\therefore 9.8\times {{10}^{8}}=-\dfrac{{{10}^{3}}\times 9.8\times h}{(-{{10}^{-3}})}\]
\[\therefore h=100m\]

So, the correct answer is “Option C”.

Note:
When the body is taken under the one medium to another medium is given by pressure difference of pressure at the top (at the surface of touching both the medium, always be the pressure of the first medium) and pressure at the depth when the body is taken (it is the sum of pressure at touching the surface and \[\rho gh\] of the second medium).