Question

The bottom, side, and front areas of a rectangular box are known. The product of these areas is equal to:
A. The volume of the box
B. The square root of the volume
C. Twice the volume
D. The square of the volume

Answer 1

Hint: To solve this question, we will assume that the rectangular box is cuboid in shape. Then we will assume length, breadth and height of this cube as l, b and h respectively. Then we will calculate the area of bottom, side and front faces by making use of the fact that these faces are rectangular in shape and we will find the areas of respective rectangles.

Complete step-by-step answer:
Before solving the question, we are going to assume that the rectangular box is cuboid in shape i.e. its faces will be perpendicular to other faces and not inclined to one other. Now let us assume that, the length of the cuboid be l, breadth be b and its height be h. Thus, we have the following cuboid:

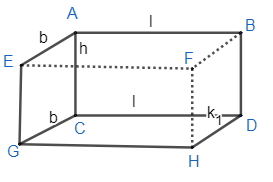
In the above figure, AB is the length, AC is the height and AE is the breadth of cuboid. From the figure, we can see that ABCD is the front face, AECG is the side face and CDHG is the bottom face. Now, the question says that we have to find the product of areas of these faces. Now, we will find the area of individual faces by making use of the fact that each face is rectangular in shape. The area of a rectangle whose dimensions a and b are given is calculated by the formula shown below:
$\text{Area}=a\times b$
Now the area of the front face will be equal to the area of rectangle ABCD which is given by:
Area of front face $=AB\times BD$
Area of front face $=l\times h$ ………………………. (1)
Similarly, the area of the side face will be equal to the area of the rectangle AEGC. Thus we have:
Area of side face $=AE\times AC$
Area of side face $=b\times h$ ……………………….. (2)
Similarly, Area of bottom face $=CD\times CG$
Area of bottom face $=b\times l$ …………. (3)
Now, the product of these faces will be obtained as:
$\left( \text{Area of front face} \right)\left( \text{Area of bottom face} \right)\left( \text{Area of side face} \right)=\left( l\times h \right)\times \left( b\times l \right)\times \left( b\times h \right)$
$\Rightarrow \text{Product of area }={{\left( l\times b\times h \right)}^{2}}$ ………………………………. (4)
Now, we will calculate the volume of the cuboid. The volume of cuboid with dimensions a, b and c is given by:
Volume $=a\times b\times c$
Thus, the volume of the cuboid is given by:
$\Rightarrow \text{Volume}=l\times b\times h$ ………………………………………………….. (5)
From (4) and (5), we have:
Product of area $={{\left( volume \right)}^{2}}$
Hence, option (d) is correct.

Note: In the question, we have assumed the rectangular box to be cuboid in shape i.e. the faces of the rectangular cuboid are either parallel to other planes or perpendicular to other plans. They cannot be inclined at some other angle. If they are inclined at some other angles, then we will not be able to develop this relation.