Question

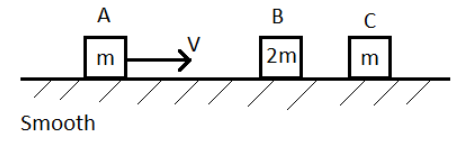
The blocks have velocities as shown in the figure. Final velocity of the block C after all possible elastic collisions is

$A)\text{ }\dfrac{8V}{9}$
$B)\text{ }V$
$C)\text{ }\dfrac{4V}{9}$
$D)\text{ }\dfrac{V}{2}$

Answer 1

Hint: This problem can be solved by considering the problem as two subproblems – one involving the elastic collision between A and B and the other the elastic collision between B and C. Using the formulae for the final velocities of a body after an elastic collision, we can get the required final velocity of C after the collision with B.
Formula used:
${{v}_{2}}=\dfrac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{2}}+\dfrac{2{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{1}}$

Complete answer:
We will consider the two elastic collisions (between A and B and subsequently between B and C) separately and use the formula for the final velocity of a body in an elastic collision in terms of the masses of the two bodies and the initial velocities of the two bodies before the collision.
For an elastic collision between two bodies 1 and 2 of masses ${{m}_{1}}$ and ${{m}_{2}}$ respectively, the final velocity of body 2 is given by
${{v}_{2}}=\dfrac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{2}}+\dfrac{2{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}{{u}_{1}}$ --(1)
Where ${{u}_{2}},{{u}_{1}}$ are the velocities of the bodies 1 and 2 just before the collision.

Now, for the collision between A and B –
The initial velocity of block $A$ is ${{u}_{A}}=V$.
The masses of A and B are ${{m}_{A}}=m$ and ${{m}_{B}}=2m$ respectively.
Since, the block B is at rest before the collision, its initial velocity is ${{u}_{B}}=0$.
Let the final velocity of the block $B$ after collision with $A$ be ${{v}_{B}}$.
Therefore, using (1), we get
${{v}_{B}}=\dfrac{{{m}_{B}}-{{m}_{A}}}{{{m}_{B}}+{{m}_{A}}}\left( {{u}_{B}} \right)+\dfrac{2{{m}_{A}}}{{{m}_{A}}+{{m}_{B}}}{{u}_{A}}$
$\therefore {{v}_{B}}=\dfrac{2m-m}{2m+m}0+\dfrac{2m}{m+2m}V=0+\dfrac{2m}{3m}V=\dfrac{2}{3}V$ --(2)
Now, the block B moves with a velocity $\dfrac{2}{3}V$ after collision with A and then goes on to hit C.
Therefore, for the collision of B with C –
The initial velocity of block $B$ is the velocity of the block B after collision with A. It is $={{v}_{B}}=\dfrac{2}{3}V$.
The masses of B and C are ${{m}_{B}}=2m$ and ${{m}_{C}}=m$ respectively.
Since the block C is at rest before the collision, its initial velocity is ${{u}_{C}}=0$.
Let the final velocity of the block $C$ after collision with $B$ be ${{v}_{C}}$.
Therefore, using (1), we get
${{v}_{C}}=\dfrac{{{m}_{C}}-{{m}_{B}}}{{{m}_{C}}+{{m}_{B}}}\left( {{u}_{C}} \right)+\dfrac{2{{m}_{B}}}{{{m}_{B}}+{{m}_{C}}}{{u}_{B}}$
$\therefore {{v}_{C}}=\dfrac{m-2m}{m+2m}0+\dfrac{2\left( 2m \right)}{2m+m}\dfrac{2}{3}V=0+\dfrac{4m}{3m}\dfrac{2}{3}V=\dfrac{8}{9}V$
Hence, we have got the required final velocity of the block C as $\dfrac{8}{9}V$.

Therefore, the correct option is $A)\text{ }\dfrac{8V}{9}$.

Note:
Students must note that in the equations for the final velocities of the bodies in the elastic collisions, that is, formula (1), the direction of motion of the bodies holds a lot of significance. For example, if two bodies are moving in the same direction before the collision, then they must be assigned velocities with the same sign (either both positive or both negative). However, if they were moving towards each other before the collision, then they must be assigned opposite signs of their speeds (one positive and the other negative).