Question

The bi-prism having an acute angle of $1{}^\circ $ and refractive index of $1.5$ is used in the interference experiment to produce two vertical slits from a single slit which is $5cm$ away from it and the screen is placed at $0.75m$ away from the bi-prism. Calculate the fringe width (in $\mu m$) if the slit is illuminated by the light of $550nm$ wavelength.

Answer 1

Hint: Bi-prism is a single prism having an apex angle slightly less than $180{}^\circ $. When a point source is used to illuminate it produces two overlapping beams of light. Bi-prism can also be said as two thin prisms placed base by base which is equivalent to a single prism.
As per the given data,
Acute angle ($\alpha $) = $1{}^\circ $
Refractive index ($\mu $) = 1.5
Distance of slit from bi-prism (a) = 5cm = $5\times {{10}^{-2}}$m
Distance of screen from bi-prism (b) = 0.75m
Wavelength of light ($\lambda $) = 550nm = $550\times {{10}^{-9}}$m
Formula used:
Separation between the two virtual slits (d),
$d=2a(\mu -1)\alpha $
Width of each fringe ($\beta $),
$\beta =\dfrac{\lambda D}{d}$

Complete answer:
The setup for the following experiment is shown here.

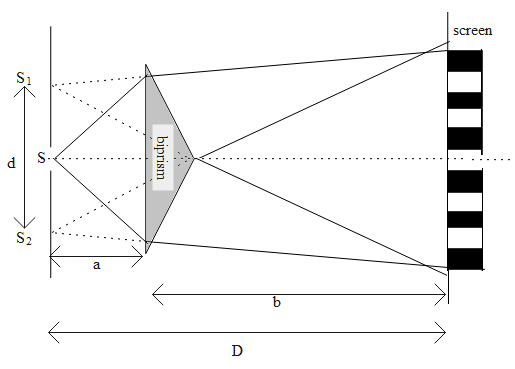
Let the separation between the two virtual slits formed by the bi-prim be $d$. The value of $d$ is dependent on the distance between the source and bi-prism, the refractive index of the prism, and the acute angle of the prism.
Mathematically,
$d=2a(\mu -1)\alpha $
Where,
$a$ is distance between the source and bi-prism
$\mu $ is refractive index of bi-prism
$\alpha $ is the acute angle of bi-prism in radian
By putting the values in the equation as per the given information,
$\begin{align}
  & d=2(5\times {{10}^{-2}})(1.5-1)\dfrac{\pi }{2} \\
 & \Rightarrow 2(0.05)(0.5)(0.0174) \\
 & \Rightarrow 8.726646\times {{10}^{-4}}m \\
\end{align}$

The total distance between the original light source and the screen is the sum of the distances of the source from the bi-prism (a) and the distance of screen from the bi-prism (b).
Mathematically,
$\begin{align}
  & D=a+b \\
 & \Rightarrow 0.05+0.75 \\
 & \Rightarrow 0.8m \\
\end{align}$
By, putting the values of a and b from the given data we found that the distance between the source and the screen is 0.8m.
When we observe the fringe pattern on the screen. Each fringe formed is of the same with irrespective of the dark or light fringe. The width of the fringe is dependent on the wavelength of the source light, the distance between the source light and the screen (D), and the distance between the source and the bi-prism.
Mathematically,
$\begin{align}
  & \beta =\dfrac{\lambda D}{d} \\
 & \Rightarrow \dfrac{550\times {{10}^{-9}}(0.8)}{8.726646\times {{10}^{-4}}} \\
 & \Rightarrow 504.202\mu m \\
\end{align}$
By using the calculated value of D and d we found that the width of each fringe produced on the screen is equivalent to $504.202\mu m$ .

Note:
A bi-prism is used to observe the diffraction pattern by two light beams using one source of light. This is done so that there is no difference between the wavelengths of both the overlapping beams. For the required calculation, the values which are used must be in the same unit and the angle should be considered in radians.