Question

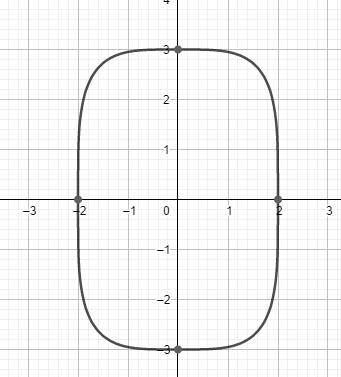
The base of a solid is the region enclosed by the curve $\dfrac{{{x}^{4}}}{16}+\dfrac{{{y}^{4}}}{81}=1$ shown in the figure above. For the solid, each cross section perpendicular to the x-axis is a semicircle. What is the volume of the solid?
A). 12.356
B). 15.732
C). 22.249
D). 49.425

Answer 1

Hint: The equation of the curve given to us is a 4-degree polynomial equation. It is also given that the curve is that of a solid figure whose cross section is perpendicular to the x-axis. Thus, we shall modify our equation and write it only in terms of the x-variable. Then, we will find the volume using integration after finding the limits of integration for x-variable.

Complete step-by-step solution:
Since, the cross-sections of the given solid are perpendicular to the x-axis, thus, we will write our equation in terms of x-variable only.
Transposing the x-term on the right-hand side and multiplying both sides by 81, we get
$\begin{align}
  & \Rightarrow \dfrac{{{y}^{4}}}{81}=1-\dfrac{{{x}^{4}}}{16} \\
 & \Rightarrow \dfrac{{{y}^{4}}}{81}=\dfrac{16-{{x}^{4}}}{16} \\
\end{align}$
$\begin{align}
  & \Rightarrow \dfrac{{{y}^{4}}}{81}\times 81=\dfrac{16-{{x}^{4}}}{16}\times 81 \\
 & \Rightarrow {{y}^{4}}=\dfrac{81}{16}\left( 16-{{x}^{4}} \right) \\
\end{align}$
Raising both the sides to the power of $\dfrac{1}{4}$, we get
$\Rightarrow y=\pm \dfrac{3}{2}{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{4}}}$ ……………………. (1)
The base of the solid was not given by the function. This implies that we shall take the intersection of the positive and negative values of the given function as the base of our curve which would be symmetric about the x-axis.
If the diameter is the entire cross-section of the semicircle, then since the radius is half of the diameter, the radius, $r$ is equal to $\dfrac{3}{2}{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{4}}}$ .
$\Rightarrow r=\dfrac{3}{2}{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{4}}}$
We also know that the area of a semicircle is half of the area of the circle with the same radius.
Area of circle $=\pi {{r}^{2}}$
Thus, area of semicircle $=\dfrac{\pi {{r}^{2}}}{2}$
Therefore, the area of semicircle, $A$ with radius, $r$ $=\dfrac{\pi }{2}{{\left( \dfrac{3}{2}{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{4}}} \right)}^{2}}$
$\Rightarrow A=\dfrac{\pi }{2}\left( \dfrac{9}{4}{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{2}}} \right)$
$\Rightarrow A=\dfrac{9\pi }{8}{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{2}}}$
In order to calculate the volume of the solid, we shall find values of x where $y=0$ and set that as the limits of integration.
Substituting $y=0$ in (1), we get
$\begin{align}
  & \Rightarrow 0=\pm \dfrac{3}{2}{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{4}}} \\
 & \Rightarrow 16-{{x}^{4}}=0 \\
\end{align}$
$\begin{align}
  & \Rightarrow {{x}^{4}}=16 \\
 & \Rightarrow {{x}^{2}}=4 \\
\end{align}$
$\Rightarrow x=\pm 2$
Therefore, the volume of the solid, $V$ is given as $\int\limits_{-2}^{2}{A}.dx$.
$\begin{align}
  & \Rightarrow V=\int\limits_{-2}^{2}{\dfrac{9\pi }{8}{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{2}}}.dx} \\
 & \Rightarrow V=\dfrac{9\pi }{8}\int\limits_{-2}^{2}{{{\left( 16-{{x}^{4}} \right)}^{\dfrac{1}{2}}}.dx} \\
 & \Rightarrow V=\dfrac{9\pi }{8}\int\limits_{-2}^{2}{\sqrt{16-{{x}^{4}}}.dx} \\
\end{align}$
Here, we see that for our function $f\left( x \right)=\sqrt{16-{{x}^{4}}}$, $\sqrt{16-{{x}^{4}}}=\sqrt{16-{{\left( -x \right)}^{4}}}$. This implies that $f\left( x \right)=f\left( -x \right)$ and $f\left( x \right)=\sqrt{16-{{x}^{4}}}$ is an even function. Therefore, we can use the property of integration, $\int\limits_{-a}^{a}{g\left( u \right).du=2\int\limits_{0}^{a}{g\left( u \right).du}}$ where $g\left( u \right)$ is any even function.
$\Rightarrow V=2\dfrac{9\pi }{8}\int\limits_{0}^{2}{\sqrt{{{4}^{2}}-{{\left( {{x}^{2}} \right)}^{2}}}.dx}$
$\Rightarrow V=\dfrac{9\pi }{4}\int\limits_{0}^{2}{\sqrt{{{4}^{2}}-{{\left( {{x}^{2}} \right)}^{2}}}.dx}$
Now using the property of integration $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}.dx=\dfrac{1}{2}\left[ x\sqrt{{{a}^{2}}-{{x}^{2}}}+{{a}^{2}}{{\sin }^{-1}}\left( \dfrac{x}{a} \right) \right]+C}$ , we get
\[\Rightarrow \int{\sqrt{{{4}^{2}}-{{\left( {{x}^{2}} \right)}^{2}}}=\dfrac{1}{2}\left[ {{x}^{2}}\sqrt{{{4}^{2}}-{{\left( {{x}^{2}} \right)}^{2}}}+{{4}^{2}}{{\sin }^{-1}}\left( \dfrac{{{x}^{2}}}{4} \right) \right]+C}\]
We shall substitute this expression in our main integration.
$\Rightarrow V=\dfrac{9\pi }{4}.\dfrac{1}{2}\left[ {{x}^{2}}\sqrt{{{4}^{2}}-{{\left( {{x}^{2}} \right)}^{2}}}+{{4}^{2}}{{\sin }^{-1}}\left( \dfrac{{{x}^{2}}}{4} \right) \right]_{0}^{2}$
Applying the limits of integration, we get
$\begin{align}
  & \Rightarrow V=\dfrac{9\pi }{8}\left\{ \left[ {{2}^{2}}\sqrt{{{4}^{2}}-{{\left( {{2}^{2}} \right)}^{2}}}+{{4}^{2}}{{\sin }^{-1}}\left( \dfrac{{{2}^{2}}}{4} \right) \right]-\left[ {{\left( 0 \right)}^{2}}\sqrt{{{4}^{2}}-{{\left( {{0}^{2}} \right)}^{2}}}+{{4}^{2}}{{\sin }^{-1}}\left( \dfrac{{{0}^{2}}}{4} \right) \right] \right\} \\
 & \Rightarrow V=\dfrac{9\pi }{8}\left\{ \left[ 4\sqrt{16-16}+16{{\sin }^{-1}}\left({1} \right) \right]-0 \right\} \\
 & \Rightarrow V=\dfrac{9\pi }{8}\left[ 0+16{{\sin }^{-1}}\left( 1 \right) \right] \\
\end{align}$
Putting the value of ${{\sin }^{-1}}1=\dfrac{\pi }{2}$, we get
 $\begin{align}
  & \Rightarrow V=\dfrac{9\pi }{8}\left[ 16\dfrac{\pi }{2} \right] \\
 & \Rightarrow V=\dfrac{9\pi }{8}\left( 8\pi \right) \\
 & \Rightarrow V=9{{\pi }^{2}} \\
\end{align}$
Also putting, $\pi =3.14$, we get
$\Rightarrow V\approx 49.425$
Therefore, the volume of the given solid is approximately 49.425.
Therefore, the correct option is (D) 49.425.

Note: In order to find the volume of a curve, it is important to visualize the curve in a 3-D plane. We must also have a good practice of using the various properties of integration which are mostly used to find the volumes of any solid. One mistake we could have made here was during the final calculations, thus, we must calculate the values carefully.