Question

The area of the triangle formed by the lines $x=0,y=0$ and $\dfrac{x}{a}+\dfrac{y}{b}=1$ is:
1. $ab$
2. $\dfrac{ab}{2}$
3. $2ab$
4. $\dfrac{ab}{3}$

Answer 1

Hint: For solving this for the straight line diagram, first of all, we should assume two lines that form the pair of equations, find the relation by multiplying the equations of these lines and comparing them with the given equations. Then using the equation of these straight lines, we can find the three points of the triangle. Now since we know the vertices of the triangle, we can calculate it’s area by using the formula, Area = $\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|$ .

Complete step-by-step solution:
According to the question it is asked to us to find the area of the triangle formed by the given lines, $x=0,y=0$ and $\dfrac{x}{a}+\dfrac{y}{b}=1$. Here we can see that the lines are given to us as $x=0,y=0$ and it is clear that both of these lines are x-axis and y-axis respectively. And both of these meet at (0, 0) and the third line which is given is $\dfrac{x}{a}+\dfrac{y}{b}=1$.
Here the $x$ intercept is $a$, and the $y$ intercept is given as $b$. So, the coordinates of the triangle are $\left( 0,0 \right),\left( a,0 \right),\left( 0,b \right)$. So, the triangle here is a right angle triangle.

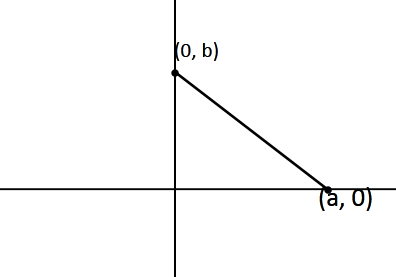
And the base of this triangle = $a$
And the height of this triangle = $b$
Since, area of triangle = $\dfrac{1}{2}\times base\times height$,
$\begin{align}
  & =\dfrac{1}{2}\times a\times b \\
 & =\dfrac{ab}{2} \\
\end{align}$
Hence the correct answer is option 2.

Note: For the random point triangle, we must note that the figure is just schematic and not to scale. While calculating the area, we must not forget about the modulus sign. This problem involves a lot of calculations, so we must write each step carefully and avoid mistakes.