Question

The area of the region described by \[A=\left\{ \left( x,y \right)={{x}^{2}}+{{y}^{2}}\le 1 \right\}\text{ and }\left\{ {{y}^{2}}\le 1-x \right\}\] is
\[\begin{align}
  & A.\dfrac{\pi }{2}+\dfrac{4}{3} \\
 & B.\dfrac{\pi }{2}-\dfrac{4}{3} \\
 & C.\dfrac{\pi }{2}-\dfrac{2}{3} \\
 & D.\dfrac{\pi }{2}+\dfrac{2}{3} \\
\end{align}\]

Answer 1

Hint: To solve this question, first we will separately draw figure and shaded region of \[\left\{ {{x}^{2}}+{{y}^{2}}\le 1 \right\}\text{ and }\left\{ {{y}^{2}}\le 1-x \right\}\] then merge them to get the common region between them. Then, observing the region obtained we can easily find the area by using integration formula given as
\[\int{\sqrt{1-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{1-{{x}^{2}}}+\dfrac{1}{2}{{\sin }^{-1}}x\text{ and }\int{\sqrt{1-x}}dx=\dfrac{2}{3}{{\left( 1-x \right)}^{\dfrac{3}{2}}}\]
Standard equation of circle is ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ where r is radius of circle and standard equation of parabola is ${{y}^{2}}=4ax$

Complete step-by-step solution:
Given that, \[{{x}^{2}}+{{y}^{2}}\le 1\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)}\]
This is an equation of a circle and inside of it having radius 1. It can be drawn as:

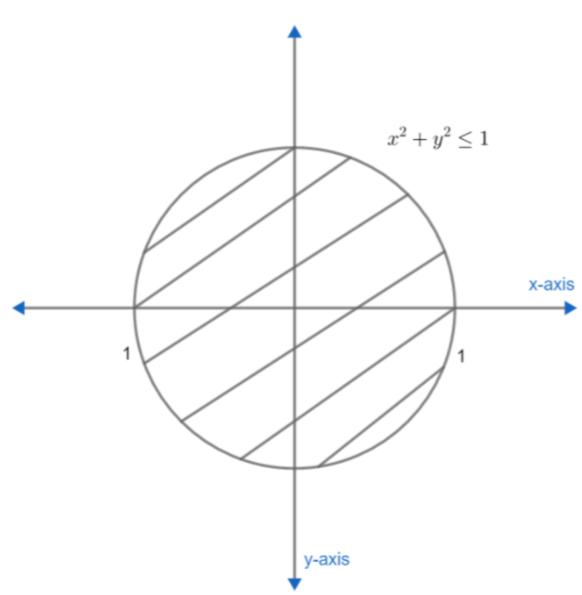
The second figure is \[{{y}^{2}}\le 1-x\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (ii)}\]
This curve represents a parabola which is symmetric about negative x-axis and vertex is (1, 0) then it can be drawn as: also \[{{y}^{2}}\le 1-x\] gives region inside of parabola.

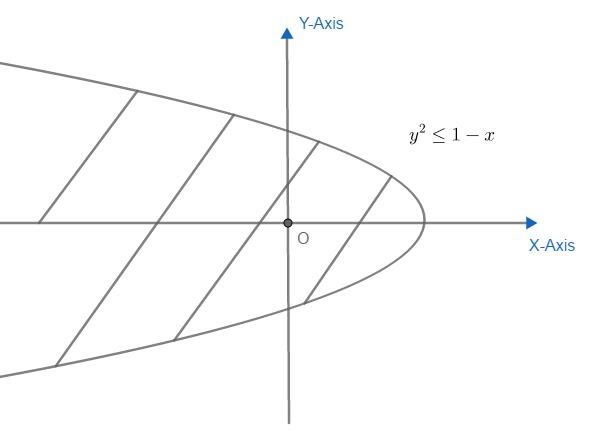
Because putting $\left( x,y \right)=\left( 0,0 \right)$ gives $0\le 1$ which is correct. So, (0, 0) comes inside region.
Now, we will merge the graph obtained of equation (i) and equation (ii):
Then, it looks like; the common region is given as

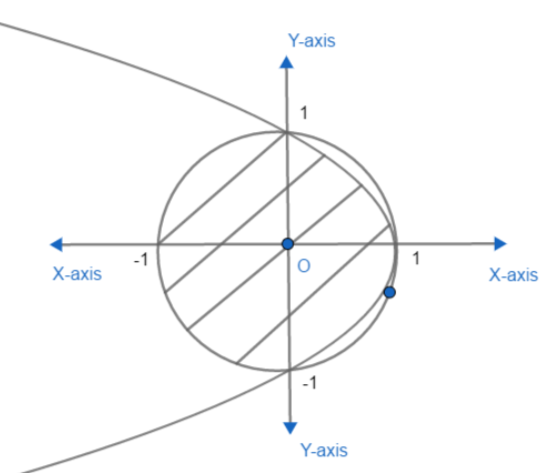
Area of the required region can be obtained by subtracting area of outer portion (the portion of circle which is not shaded) to area of circle.
\[\text{A }=\text{ area of circle }-\text{ area of outer portion of circle }.\text{ }.\text{ }.\text{ }.\text{ }.\text{ }\left( \text{iii} \right)\]
Area of circle of radius r is given by $\pi {{r}^{2}}$
Here, r = 1 then area of circle \[\pi {{\left( 1 \right)}^{2}}\Rightarrow \pi \]
Now, to find area of outer portion of circle, we will first calculate the area of outer portion which is above x-axis and then multiply it by 2 as both above and lower portion are symmetric.
Area of outer portion \[\Rightarrow 2\times \int\limits_{0}^{1}{\text{circle - parabola}}\]
Area of outer portion \[\Rightarrow 2\times \int\limits_{0}^{1}{\text{circle equation - parabola}}\]
We have ${{x}^{2}}+{{y}^{2}}=1$ is circumference of circle.
\[\Rightarrow {{y}^{2}}=1-{{x}^{2}}\]
Taking square root \[\Rightarrow y=\sqrt{1-{{x}^{2}}}\]
So this is the required value of y for circle. Here, only $+\sqrt{1-{{x}^{2}}}$ is considered as we are calculating for the above portion of the circle.
Now, for parabola \[\Rightarrow {{y}^{2}}=1-x\]
Taking square root \[\Rightarrow y=\sqrt{1-x}\]
This is the value of y for the parabola.
Substituting both y values for area of outer circle, we get:
Area of outer circle \[\Rightarrow 2\times \int\limits_{0}^{1}{\left( \sqrt{1-{{x}^{2}}}-\sqrt{1-x} \right)}dx\]
Now, formula of integration of $\sqrt{1-{{x}^{2}}}$ is
\[\begin{align}
 & \Rightarrow \int\limits_{0}^{1}{\sqrt{1-{{x}^{2}}}}dx=\left( \dfrac{x}{2}\sqrt{1-{{x}^{2}}}+\dfrac{1}{2}{{\sin }^{-1}}x \right)_{0}^{1}{{}}\text{ and } \\
 & \int\limits_{0}^{1}{\sqrt{1-x}dx=\int\limits_{0}^{1}{{{\left( 1-x \right)}^{\dfrac{1}{2}}}dx}} \\
 & \Rightarrow \left( \dfrac{{{\left( 1-x \right)}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1}\right)_{0}^{1}{{}} \\
 & \Rightarrow \int{\sqrt{1-x}dx= -\dfrac{2}{3}{{\left( 1-x \right)}^{\dfrac{3}{2}}}} \\
\end{align}\]
Using these both values in above we get:
Area of outer circle \[\Rightarrow 2\times \left( \dfrac{x}{2}\sqrt{1-{{x}^{2}}}+\dfrac{1}{2}{{\sin }^{-1}}x+\dfrac{2}{3}{{\left( 1-x \right)}^{\dfrac{3}{2}}} \right)_{0}^{1}\]
Area of outer circle \[\Rightarrow 2\left( \dfrac{1}{2}\sqrt{1-1}+\dfrac{1}{2}{{\sin }^{-1}}1+\dfrac{2}{3}{{\left( 1-1 \right)}^{\dfrac{3}{2}}}-0- \dfrac{1}{2}{{\sin }^{-1}}0-\dfrac{2}{3}{{\left( 1-0 \right)}^{\dfrac{3}{2}}} \right)\]
Area of outer circle \[\Rightarrow 2\times \dfrac{1}{2}\times \dfrac{\pi }{2}-\dfrac{2}{3}\times 2\]
Area of outer circle $\Rightarrow \dfrac{\pi }{2}-\dfrac{4}{3}$
Finally, we will calculate area of required region A. Substituting the value of area of circle and area of outer circle obtained above in equation (iii) we get:
\[\begin{align}
  & \text{Area = }\pi \text{-}\left( \dfrac{\pi }{2}-\dfrac{4}{3} \right) \\
 & \Rightarrow \pi -\dfrac{\pi }{2}+\dfrac{4}{3} \\
 & \Rightarrow \dfrac{\pi }{2}+\dfrac{4}{3} \\
\end{align}\]
Hence, the value of area of given region is $A=\dfrac{\pi }{2}+\dfrac{4}{3}$ which is option A.

Note: Confusion can arise at the point where we have to determine whether the region outer of the parabola is to be considered or inside of it. In such cases, put $\left( x,y \right)=\left( 0,0 \right)$ and check that whether it is satisfied or not. If it is satisfied then the region having (0, 0) is correct otherwise the other region left is possible.
Also, there is one more key point in this question, at the place where we are considering \[y=+\sqrt{1-{{x}^{2}}}\] for finding the area of the circle. Even if you proceed to select the negative part that is \[y=-\sqrt{1-{{x}^{2}}}\] then also you have to make it positive as the area of any region is never negative.