Question

The area of the region bounded by $y=x$ , $y={{x}^{3}}$ is?

Answer 1

Hint: In the given question we are asked to find the area bounded by two continuous curves which we can firstly plot on the graph and then find the shaded region and further proceed to find the area. We need to use integration in this question and limits would be the intersection points of both the curves and can be done easily.

Complete step by step solution:
According to the given question, we need to plot two curves. First curve is $y=x$ and second curve is $y={{x}^{3}}$ .
So, the graph of the two curves and their intersection is shown below:
                   

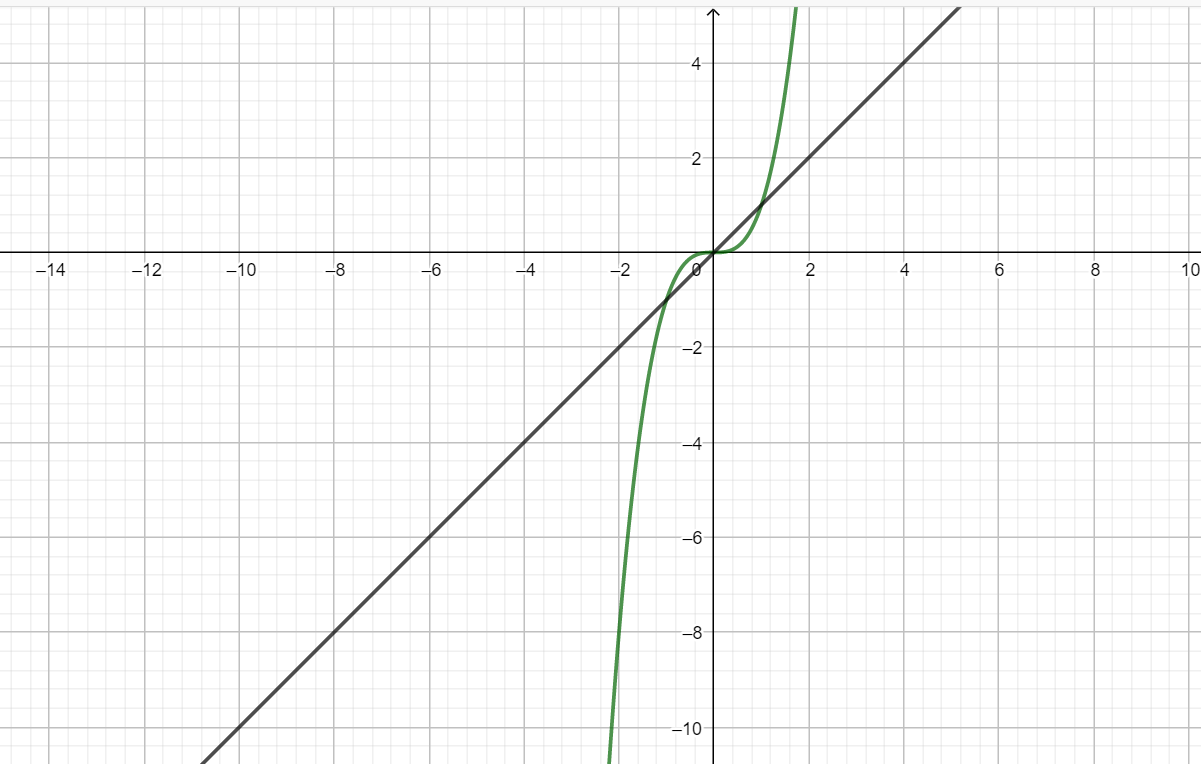
Now, we can clearly see that the curve $y={{x}^{3}}$intersects the line $y=x$ thrice. So, the points at which the two curves are intersecting are (0,0), (1,1), (-1,-1).
Now, in order to find the area, we can find the area of both the shaded curves separately, also, we can find the area of the one portion and then multiply by 2 as it is symmetrical.
Now, the area between two curves is:
$\begin{align}
  & A=\int\limits_{0}^{1}{\left( {{x}^{3}}-x \right)}dx \\
 & \Rightarrow A=\left( \dfrac{{{x}^{4}}}{4}-\dfrac{{{x}^{2}}}{2} \right)_{0}^{1} \\
 & \Rightarrow A=\dfrac{1}{4}-\dfrac{1}{2}-0 \\
 & \Rightarrow A=\dfrac{-1}{4} \\
\end{align}$
Now, we will remove the minus sign as area can never be negative but the magnitude will remain the same and for the complete area, we will multiply our answer by 2 and we get $\dfrac{1}{2}$ .
Therefore, the area between the two curves is $\dfrac{1}{2}$sq.units.

Note: In such questions make the plot correctly in such a way that the coordinates lie in the correct quadrant and then carefully find the limits of integration after finding the intersection points of the curves. Also, the upper limit and lower limit must be carefully found. Also, find the area of the specified region only as in the given question we need to find the area of complete shaded region between two curves.