Question

The area of the region bounded by the curves \[{\rm{y = ex log x}}\] and\[{\rm{y = }}\dfrac{{{\rm{log x}}}}{{{\rm{ex}}}}\] is
A) \[\dfrac{{{{\rm{e}}^2} - 5}}{{4{\rm{e}}}}\]
B) \[{\rm{e}} - \dfrac{5}{4}\]
C) \[\dfrac{{\rm{e}}}{4} - 5\]
D) \[\dfrac{{\rm{e}}}{4} - \dfrac{1}{{4{\rm{e}}}}\]

Answer 1

Hint:
Here in this question we will use the integration to find out the area bounded by the curves. So firstly we will find out the intersection points of the curves to define the limit of the integration. Then after that we will apply limits to the area bounded by both the curves and by simple integration we will be able to get the required bounded area.

Complete step by step solution:
Equation of the given curves are\[{\rm{y = ex log x}}\] and\[{\rm{y = }}\dfrac{{{\rm{log x}}}}{{{\rm{ex}}}}\].
Now we have to find the intersection points of the curves by simply equating the equation of both the curves, we get
\[ \Rightarrow {\rm{ex log x = }}\dfrac{{{\rm{log x}}}}{{{\rm{ex}}}}\]
\[ \Rightarrow ({{\rm{e}}^2}{{\rm{x}}^2}{\rm{ - 1)}} \times {\rm{log x = 0}}\]
By solving the above equation we will get the value of x as \[{\rm{x = 1,}}\dfrac{1}{{\rm{e}}}\]

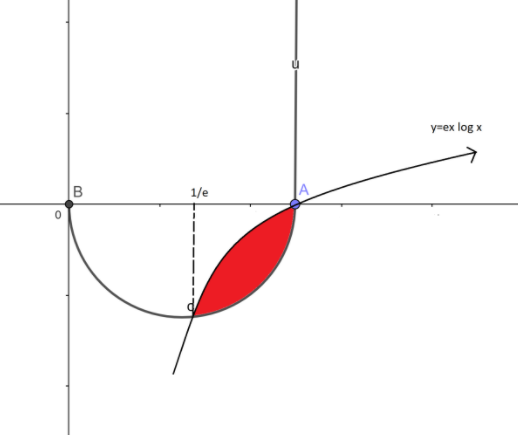
Now we apply the limits to the required area, we get
Required area\[ = \int\limits_{\dfrac{1}{{\rm{e}}}}^1 {\left( {\dfrac{{{\rm{log x}}}}{{{\rm{ex}}}} - {\rm{ex log x}}} \right)} {\rm{dx}}\]
Now by simply applying integration we will get the bounded area. Therefore, solving the above equation
Required area \[ = \dfrac{1}{{\rm{e}}}\int\limits_{\dfrac{1}{{\rm{e}}}}^1 {\left( {\dfrac{{{\rm{log x}}}}{{\rm{x}}}{\rm{dx}}} \right) - {\rm{e}}\int\limits_{\dfrac{1}{{\rm{e}}}}^1 {\left( {{\rm{x log x}}} \right)} } {\rm{dx}} = \dfrac{1}{{\rm{e}}} \times \left( {\dfrac{{{{{\rm{(log x)}}}^2}}}{2}} \right)_{\dfrac{1}{{\rm{e}}}}^1 - {\rm{e}} \times \left( {{\rm{log x }} \times \dfrac{{{{\rm{x}}^2}}}{2} - \dfrac{1}{4}{{\rm{x}}^2}} \right)_{\dfrac{1}{{\rm{e}}}}^1\]
By solving the equation we will get,
Required area \[ = \dfrac{{\rm{e}}}{4} - \dfrac{5}{{4{\rm{e}}}} = \dfrac{{{{\rm{e}}^2} - 5}}{{4{\rm{e}}}}\]

Hence, \[\dfrac{{{{\rm{e}}^2} - 5}}{{4{\rm{e}}}}\]is the bounded area by the curves
So, option A is correct.

Note:
Area is the amount of surface covered by a shape in two dimensional. The area which is enclosed between two curves or shapes is known as the bounded region or bounded area. We should be knowing the method of integration. In almost all of the bounded area problems we have to use the integration method to find out the area. In the above problem we used the integration about the x axis but we can also integrate the area about the y axis but then we have to find the value of intersection in terms of y coordinates.