Question

The area of the rectangle is \[300\] cm squared. What is the length and width of the ratio of the length to width is \[4:3\]?

Answer 1

Hint: In this question, given that the area of the rectangle is \[300\] cm squared. We need to find out the length and width of the rectangle where the ratio of the length to width is \[4:3\] . First we can turn the given ratio into a mathematical equation .Then we can find the width by using the area of the rectangle formula. After finding the width we can easily find the length of the rectangle by using the given ratio.

Complete step by step solution:
Given the area of the rectangle is \[300\] cm squared and also the ratio of the length to width ( which we can shorten as \[L\] and \[W\] for our convince) is \[4:3\] which means length divided by width is equal to \[4\] divided by \[3\] and we can turn that in to mathematical equation, \[\dfrac{L}{W} = \dfrac{4}{3}\]
From which \[L = \dfrac{4}{3}W\] ••• (1)

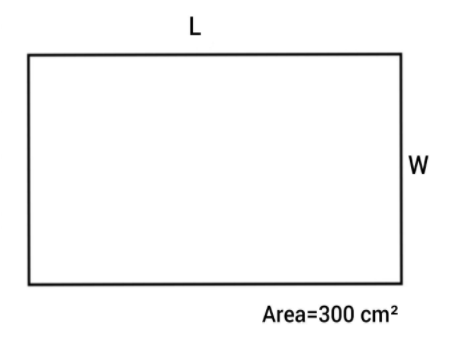
We know that the formula of the area of the rectangle is the product of its length and width of the rectangle.
\[A = L \times W\]
Given that the area of the rectangle is \[300\] cm squared.
\[\Rightarrow \ L \times W = 300\]
Now on substituting \[L = \dfrac{4}{3}W\] ,
We get,
\[\Rightarrow \dfrac{4W}{3} \times W = 300\]
On keeping constant at side and moving other terms to opposite side,
We get,
\[\Rightarrow \ W^{2} = \dfrac{300 \times 3}{4}\]
On simplifying,
We get,
\[\Rightarrow \ W^{2} = \dfrac{900}{4}\]
On dividing,
We get,
\[\Rightarrow \ W^{2} = 225\]
On taking square root on both sides,
We get,
\[\ W = \sqrt{225}\]
On simplifying,
We get,
\[\Rightarrow \ W = 15\]
(We have ignored the negative root since that makes no sense in this application)
Thus we get the width of the rectangle is \[15\] cm.
Now we can substitute the value of \[W\] in equation (1) ,
We get,
\[L = \dfrac{4}{3}\left( 15 \right)\]
On simplifying,
We get,
\[\Rightarrow \ L = 4 \times 5\]
On multiplying,
We get,
\[\Rightarrow \ L = 20\]
Thus we get the length of the rectangle is \[20\] cm.
Therefore the length and width of the rectangle is \[20\] cm and \[15\] cm respectively.
The length and width of the rectangle is \[20\] cm and \[15\] cm respectively.


Note:
A rectangle is nothing but a two dimensional shape having four sides and four corners. The area of the rectangle is given by the product of its adjacent sides whereas the perimeter of a rectangle is the sum of the length of its four sides. While solving these questions, we should know all the formulas , otherwise the question could not be solved because the use of the formula is the only way to solve it. We can also solve the same problem by substituting \[L\] instead of \[W\]. We can also check whether our answer is correct or not by multiplying the length and width. If the product of our length and width is \[300 \ cm^{2}\] , then our answer is absolutely correct.