Question

The area of the quadrilateral in a circle is maximum when the quadrilateral is:
(a) rectangle
(b) square
(c) parallelogram
(d) rhombus

Answer 1

Hint: We will opt option verification method for this question, we will consider all the options and first eliminate which are not possible. We will then draw a general figure which satisfies the remaining option. Then, we will see which of the remaining options will have maximum area for given lengths of their diagonals.

Complete step by step answer:
Without the loss of generality, we assume that ABCD are the vertices of a quadrilateral.
Now, suppose the quadrilateral is a parallelogram.
We know that the opposite angles of a parallelogram are equal.
$\Rightarrow $ ∠A = ∠C
$\Rightarrow $ ∠B = ∠D
We also know that for any cyclic quadrilateral (quadrilateral inscribed in a circle), sum of opposite angles is 180°.
$\Rightarrow $ ∠A + ∠C = 180°
$\Rightarrow $ ∠B + ∠D = 180°
But we have already shown that the opposite angles of a parallelogram are equal.
$\Rightarrow $ ∠A + ∠A = 180°
$\Rightarrow $ 2∠A = 180°
$\Rightarrow $ ∠A = 90°
$\Rightarrow $ ∠C = 90°
$\Rightarrow $ ∠B = 90°
$\Rightarrow $ ∠D = 90°
Therefore, we can safely say that ABCD is either a rectangle or a square, since parallelogram and rhombus do not have any angle as 90°.
Now, let us draw a figure of a square and rectangle inscribed in a circle.

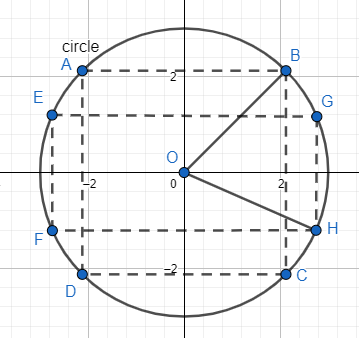
As we can see, let ABCD be the square and EFGH be the rectangle inscribed in a circle.
We will compare the area of both figures who have the same length of diagonals. Since, the distance from the centre of the circle and the vertices on the circumference is equal to the radius.
Therefore, the length of all the diagonals is the same and equal to the diameter of the circle.
Now, the area of the square is twice that of the area of triangle ABD.
Similarly, the area of the rectangle is twice that of the area of triangle GEF.
In triangle ABD, the base of the triangle is diagonal BD. The height will be equal to the radius as we know that the diagonals of a square are at right angles.
Hence, the area of the triangle ABD = $\dfrac{1}{2}\times d\times \dfrac{d}{2}=\dfrac{{{d}^{2}}}{4}$.
Area of the square ABCD = $2\times \dfrac{{{d}^{2}}}{4}=\dfrac{{{d}^{2}}}{2}$.
Now, in the triangle GEF, the base is diagonal GE. The height of the triangle will be the product of radius and sine of the angle between the diagonals. This is because the diagonals are not at right angles and hence cannot be considered altitudes.
Hence, the area of the triangle GEF = $\dfrac{1}{2}\times d\times \dfrac{d}{2}\times \sin \left( y \right)=\dfrac{{{d}^{2}}}{4}\sin \theta $, where $\theta $ is the angle between the two diagonals in the range (0°, 90°).
Area of the rectangle GEFH = $2\times \dfrac{{{d}^{2}}}{4}\sin \theta =\dfrac{{{d}^{2}}}{2}\sin \theta $
But we know that the value of sin$\theta $ lies between 0 and 1.
Therefore, the area of the square is always more than the area of the rectangle when inscribed in a circle.

So, the correct answer is “Option B”.

Note: Students can directly remember that area of any quadrilateral can be given by the relation $A={{d}_{1}}{{d}_{2}}\sin \left( y \right)$, where ${{d}_{1}}$ and ${{d}_{2}}$ are the lengths of their diagonals and y is the angle between the diagonals.