Question

The area of a square field is \[3200{m^2}\]. How long will a lady take to cross the field diagonally at the rate of \[3.3km/hr\]?
A. 1hour25minutes
B. 1hour15minutes
C. 1hour35minutes
D. 1hour45minutes

Answer 1

Hint: We will first consider the given data as the area of the square is given by \[{a^2}\]. We can find the length of the diagonal of a square by finding the value of \[{d^2}\] which is equal to twice the area of the square. We can simplify the expression and find the value of the diagonal. We have found the distance and as the rate is given, we can find the time using the distance-time relationship.

Complete step by step answer:

We will first consider the given data that is the area of the square is given by \[{a^2} = 3200\].
We need to find the time taken by the lady to cross the field diagonally at the given rate.
Now, the length of the diagonal of a square, \[d\] can be found by putting it equal to twice the area of the square.
We will consider the figure,

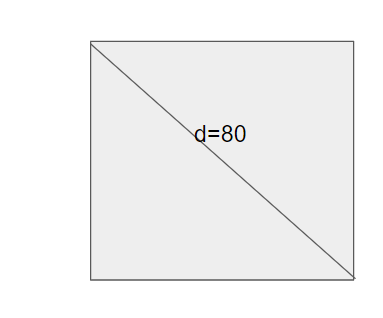
Thus, we get,
\[
   \Rightarrow {d^2} = 2{a^2} \\
   \Rightarrow {d^2} = 2\left( {3200} \right) \\
   \Rightarrow {d^2} = 6400 \\
   \Rightarrow d = 80 \\
 \]
Hence, the length of the diagonal is 80 m
Now, as we have to find the time taken to cross a length of 80 meters while travelling at \[3.3km/hr\] can be found by using the distance-time relationship that is \[T = \dfrac{d}{r}\].
Also, we need to convert the unit of rate the same as the unit of length of diagonal by multiplying the expression by \[\dfrac{{60}}{{1000}}\] to convert the \[km/hr\] into \[m/\min \].
Thus, we have,
\[
   \Rightarrow T = \dfrac{{80}}{{3.3}} \times \dfrac{{60}}{{1000}} \\
   \Rightarrow T = 1{\text{ hour 45 minutes}} \\
 \]
Hence, we get the time taken by the lady is \[1{\text{ hour 45 minutes}}\].
Thus, option D is correct.

Note: We have to convert the units from \[km/hr\] into \[m/\min \]. We have used the distance-time relationship concept by comparing the distance with the length of the diagonal, velocity with the rate and time as it is. We have used the fact that the length of the diagonal is the same as twice the area of the square and simplifies to find the length. We can also find the length of the diagonals by using Pythagoras theorem as the sides of the square are the same so using the area of the square, we can evaluate the side of the square.