Question

The area of a rhombus is \[48c{m^2}\]. One of its diagonals measures 8 cm. What is the length of the diagonal?

Answer 1

Hint: We will assume the length of the diagonal to be x. Then put in all the known values in the formula for the area of rhombus and then find the value of x to get the desired length of the diagonal.

Formula Used:
The area of rhombus is given by:
\[area = \dfrac{1}{2} \times \left( {{\text{length of diagonal 1}}} \right) \times \left( {{\text{length of diagonal 2}}} \right)\]

Complete step by step solution:

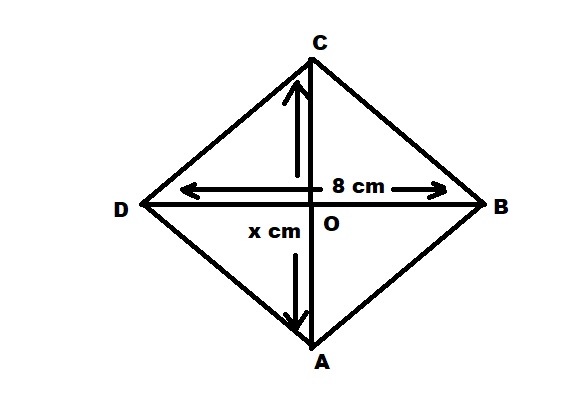
Here it is given that area of the rhombus is \[48c{m^2}\].
Also, the length of diagonal 1 is 8cm.
Let the length of diagonal 2 be $x$.
Now as we know that the area of rhombus is given by:
\[area = \dfrac{1}{2} \times \left( {{\text{length of diagonal 1}}} \right) \times \left( {{\text{length of diagonal 2}}} \right)\]
Putting in the respective values we get:
\[ \Rightarrow 48 = \dfrac{1}{2} \times 8 \times x\]
On simplification of he above values,
$\Rightarrow48 = 4x $
Dividing the whole equation by 4 to get the value of x:
\[ x = \dfrac{{48}}{4}\]
On simplification, we get
$\Rightarrow x = 12cm$

$\therefore$ The length of another diagonal is 12 cm.

Note:
Let the length of other diagonal (AC) be $x$.
The length of another diagonal can also be calculated by calculating the area of each triangle formed by the diagonals and then adding them to get the desired value of length(x).
Since the diagonals of a rhombus are perpendicular to each other and bisect each other.
Therefore,
\[ar\left( {\Delta AOB} \right) = ar\left( {\Delta BOC} \right) = ar\left( {\Delta COD} \right) = ar\left( {\Delta DOA} \right)\]
This implies that the area of rhombus is given by:-
\[ar\left( {ABCD} \right) = 4ar\left( {\Delta AOB} \right)\]………………………..(1)
Since the area of rhombus is given as \[48c{m^2}\]
Therefore putting value in equation 1 we get:
\[48 = 4ar\left( {\Delta AOB} \right)\]…………………………(2)
Now we need to calculate the area of \[\Delta AOB\].
Now since we know that the area of a triangle is given by:-
\[area = \dfrac{1}{2} \times base \times height\]
Also since the diagonals of a rhombus bisect each other
Therefore,
\[
OA = OC = \dfrac{x}{2} \\
OB = OD = 4cm \\
 \]
Now in \[\Delta AOB\]
\[
base = OB = 4cm \\
height = OA = \dfrac{x}{2} \\
 \]
Hence putting in the values in the formula of the area we get:-
\[
ar\left( {\Delta AOB} \right) = \dfrac{1}{2} \times 4 \times \dfrac{x}{2} \\
 \Rightarrow ar\left( {\Delta AOB} \right) = x \\
 \]
Now putting this value in equation 2 we get:-
\[
48 = 4x \\
 \Rightarrow x = \dfrac{{48}}{4} \\
 \Rightarrow x = 12cm \\
 \]
Therefore the length of another diagonal is 12 cm.