Question

The area of a rectangle gets reduced by 9 square units if its length is reduced by 5 units and the breadth is increased by 3 units. If we increase the length by 3 units and breadth by 2 units, the area is increased by 67 square units. Find the length and breadth of the rectangle.
17 and 10
17 and 19
17 and 39
None of these

Answer 1

Hint: Start by assuming the length of rectangle = x units, and the breadth of rectangle = y units. Apply the formula for the area. Use the statements given in the question to form new relation of length, breadth, and area. Equate the relation found in order to obtain values of x and y.

Complete step-by-step solution:
Let the length and breadth of the rectangle be x unit and y unit.
Now the area of the rectangle, $A = xy$.
Now, According to the statement given in the question, we have
The length is reduced by 5 units and the breadth is increased by 3 units. And the area has decreased by 9 units.

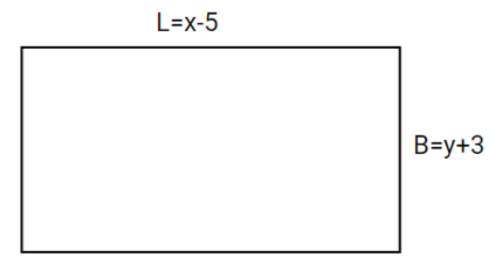
So , the new length will be =$x - 5$
So , the new breadth will be =$y + 3$
New area = $xy - 9$
So, the new the relation will be
$
  (x - 5)(y + 3) = xy - 9 \\
   \Rightarrow 3x - 5y - 6 = 0 \to eqn(1) \\
$
Also, when the length is increased by 3 units and the breadth is increased by 2 units, then the area Is increased by 67 units.

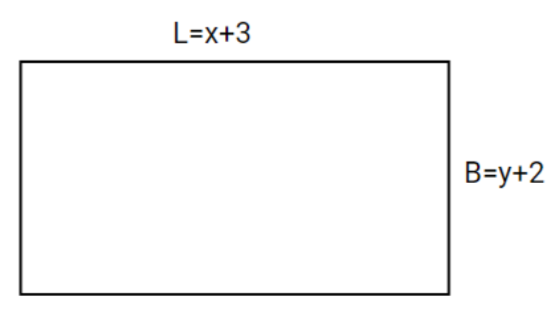
New length = $x + 3$
New breadth will be =$y + 2$
New area = $xy + 67$
So, the new the relation will be
$
  (x + 3)(y + 2) = xy + 67 \\
   \Rightarrow 2x + 3y - 61 = 0 \to eqn(2) \\
$
We know, cross – multiplication method
$\begin{array}{*{20}{c}}
  {{a_1}x + {b_1}y + {c_1} = 0} \\
  {{a_2}x + {b_2}y + {c_2} = 0}
\end{array}$
Then they can be solved by using the relation
$
  \dfrac{x}{{{b_1}{c_2} - {b_2}{c_1}}} = \dfrac{y}{{{a_2}{c_1} - {c_2}{a_1}}} = \dfrac{1}{{{a_1}{b_2} - {a_2}{b_1}}} \\
  x = \dfrac{{{b_1}{c_2} - {b_2}{c_1}}}{{{a_1}{b_2} - {a_2}{b_1}}},y = \dfrac{{{a_2}{c_1} - {c_2}{a_1}}}{{{a_1}{b_2} - {a_2}{b_1}}} \\
$
$
   \Rightarrow \dfrac{x}{{305 - ( - 18)}} = \dfrac{y}{{ - 12 - ( - 183)}} = \dfrac{1}{{9 - ( - 10)}} \\
   \Rightarrow \dfrac{x}{{323}} = \dfrac{y}{{171}} = \dfrac{1}{{19}} \\
   \Rightarrow x = 17,y = 9 \\
$
Therefore, the length of the rectangle = 17 units.
The breadth of the rectangle = 9 units.
Hence, the correct option is D. None of these.

Note: Whenever such types of questions appear, write down the values given in the question. And then assume length and breadth of the rectangle be x and y, then also, the area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units, as given in the question, form the equation using the conditions given in the question and solve the question.