Question

The area in square units of the region $A=\{(x,y):{{x}^{2}}\le y\le x+2\}$ is?
(a) $\dfrac{10}{3}$
(b) $\dfrac{9}{2}$
(c) $\dfrac{31}{6}$
(d) $\dfrac{13}{6}$

Answer 1

Hint: To solve this question, first we will solve for the values of x, for which values of y are the same. Then, we will integrate the function with limits according to values of x obtained as we know that the area under the curve is equal to integration of the function of the curve from upper limit to lower limit.

Complete step by step answer:
Now, in question it is given that $A=\{(x,y):{{x}^{2}}\le y\le x+2\}$and we have to evaluate the area under this curve in square units.
Now, we have ${{x}^{2}}\le y\le x+2$
So, we have two functions, which are $y=x+2$ and $y={{x}^{2}}$.
Now, first we see what are the points of x at which these curves intersect each other.
So, as where curves intersect, we have the same output.
Then, \[y={{x}^{2}}=x+2\]
On solving, we get
\[{{x}^{2}}-x-2=0\]
On factorising, we get
\[{{x}^{2}}-2x+x-2=0\]
\[x(x-2)+(x-2)=0\]
\[(x+1)(x-2)=0\]
So, we have two values o x, which are x = 2, - 1 .

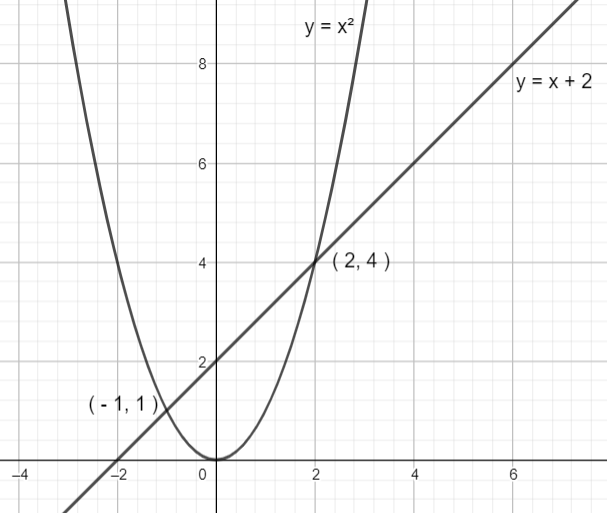
When we have, two functions say f( x ) and g( x ) where f( x ) > g( x ) and they intersect at points say x = a and x = b then area under the curves will be $\int\limits_{x=a}^{x=b}{\left( f(x)-g(x) \right)}dx$ .
So, from graph we can say that $x+2>{{x}^{2}}$ from x = -1 to x = 2
So, Area A $=\int\limits_{-1}^{2}{\{(x+2)-{{x}^{2}}\}dx}$
\[={{\{\dfrac{{{x}^{2}}}{2}+2x-\dfrac{{{x}^{3}}}{3}\}}_{-1}}^{2}\]
\[=\left( \dfrac{{{(2)}^{2}}}{2}+2(2)-\dfrac{{{(2)}^{3}}}{3} \right)-\left( \dfrac{{{(-1)}^{2}}}{2}+2(-1)-\dfrac{{{(-1)}^{3}}}{3} \right)\]
\[=2+4-\dfrac{8}{3}-\dfrac{1}{2}+2-\dfrac{1}{3}\]
\[=\dfrac{9}{2}\]
So, area of region $A=\{(x,y):{{x}^{2}}\le y\le x+2\}$ is equals to \[\dfrac{9}{2}\]sq. units.

So, the correct answer is “Option B”.

Note: To solve questions related to area of curve, one must know the concept of area between two curves and must know how to draw graphs of the curves. Calculation must be avoided while solving the question. unit should be written after the final numerical answer.