Question

The area (in square units) bounded by the curves \[y=\sqrt{x}\], \[2y-x+3=0\] and x-axis lying in the first quadrant is:
A. \[9\]
B. \[36\]
C. \[18\]
D. \[{}^{27}/{}_{4}\]

Answer 1

Hint: Observe the relation \[y=\sqrt{x}\], with the parabola \[{{y}^{2}}=4ax\] by squaring \[y=\sqrt{x}\] to both sides. Find the intersection of \[y=\sqrt{x}\] and \[2y-x+3=0\] and represent the bounded area with the given curves in the first quadrant only. Area of \[y=f(x)\] from x =a to x = b under x-axis is given by relation \[=\int\limits_{a}^{b}{f(x)dx}\].

Complete step by step answer:
Here, we have curves in the problem as,
\[\begin{align}
  & y=\sqrt{x} \\
 & 2y-x+3=0 \\
\end{align}\]
and x-axis
and we need to determine the area bounded by these curves in the first quadrant only. So we need to plot these curves on the coordinate axes and hence determine the region bounded by them.
As \[2y-x+3=0\] is an equation of a line, so we can represent it by taking any two values of (x, y) which satisfies it. Hence, it can be represented on the coordinate axis easily. But we need to analyse the equation \[y=\sqrt{x}\].
Squaring both sides in the equation \[y=\sqrt{x}\], we get the equation as,
\[{{y}^{2}}=x.....(1)\]
Now, compare this equation with the equation of the parabola \[{{y}^{2}}=4ax\], where value of 4a in \[{{y}^{2}}=x\] in 1. Hence the equation \[{{y}^{2}}=x\] will be a parabola.
Hence \[y=\sqrt{x}\] will also represent a parabola of type \[{{y}^{2}}=4ax\].
Hence let us represent \[y=\sqrt{x}\], \[2y-x+3=0\] curves on the coordinate axes as following:-

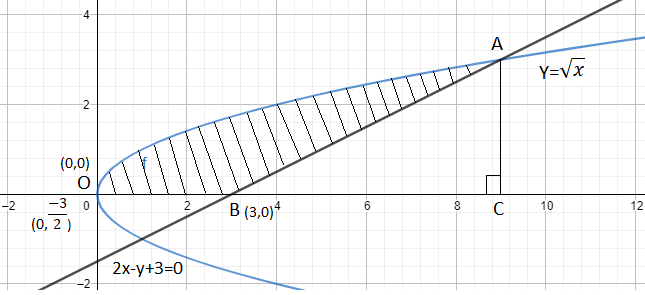
Now, we can observe that the shaded region i.e. OABO is the area bounded by the given curves in the problem. So we need to find the area of OABO by taking the difference of the area of OACO and the area of triangle ACB.
So let us first find the intersection of the curves \[y=\sqrt{x}\] and \[2y-x+3=0\] to get the coordinates of point A.
So we have,
\[\begin{align}
  & y=\sqrt{x} \\
 & {{y}^{2}}=x.....(1) \\
 & 2y-x+3=0......(2) \\
\end{align}\]
Put the value of x from equation (1) i.e. \[x={{y}^{2}}\] to the equation (2). Hence we get,
\[\begin{align}
  & 2y-x+3=0 \\
 & {{y}^{2}}-2y-3=0 \\
\end{align}\]
Now factorizing the above expression, we get,
\[\begin{align}
  & {{y}^{2}}-3y+y-3=0 \\
 & y(y-3)+1(y-3)=0 \\
 & (y-3)(y+1)=0 \\
\end{align}\]
Hence, \[y+1=0\] or \[y-3=0\]
\[y=-1\] or \[y=3\].
Now, we cannot take \[y=-1\] value as point A is lying in the first quadrant. So \[y=-1\] is another point of intersection of the curves in the 4th quadrant of the graph. So put y = 3 in the equation (2). Hence we get,
\[\begin{align}
  & 2(3)-x+3=0 \\
 & 6-x+3=0 \\
 & x=9 \\
\end{align}\]

Hence point A is given as A (9, 3).
So line AC is representing x = 9 and coordinate of C will be (9, 0).
Hence we can calculate area of triangle as,
Area of triangle \[=\dfrac{1}{2}\times base\times height....(3)\]
So we know, length AC = 3, and length BC can be given by the difference of the lengths OC and OB. Hence we get,
BC = OC – OB = 9 – 3 = 6.
\[\therefore BC=6\].
Hence area of triangle ABC with the help of equation (3) can be given as,
Area of triangle \[\Delta ABC=\dfrac{1}{2}\times 6\times 3=9uni{{t}^{2}}\]
Area of OACO can be calculated by integrating the curve \[y=\sqrt{x}\] from x = 0 to x = 9.
Hence we get, area of OACO \[=\int\limits_{0}^{9}{\sqrt{x}}dx=\int\limits_{0}^{9}{{{x}^{{}^{1}/{}_{2}}}}dx\].
We know the integration of \[{{x}^{n}}\] can be given as,
\[\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}\]
Hence we get,
Area of OACO \[=\int\limits_{0}^{9}{{{x}^{{}^{1}/{}_{2}}}}dx=\left[ \dfrac{{{x}^{{}^{1}/{}_{2}}}+1}{\left( \dfrac{1}{2}+1 \right)} \right]_{0}^{9}\]
\[=\left[ \dfrac{{{x}^{{}^{3}/{}_{2}}}}{{}^{3}/{}_{2}} \right]_{0}^{9}=\dfrac{2}{3}\left[ \left( {{x}^{{}^{3}/{}_{2}}} \right) \right]_{0}^{9}=\dfrac{2}{3}\left[ {{\left( 9 \right)}^{{}^{3}/{}_{2}}}-0 \right]=\dfrac{2}{3}{{\left( 3 \right)}^{3}}=\dfrac{2}{3}\times 27=18uni{{t}^{2}}\]
Hence area of the shaded region can be given as area of the shaded region = 18 – 9 = 9.
So the area of the bounded region \[=9uni{{t}^{2}}\].
So option A is the correct answer.

Note:
We can get the area of the shaded region with respect to the y-axis as well.

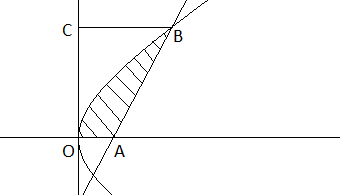
We need to find area of OABC by integrating \[x={{y}^{2}}\] with respect to dy and area of trapezium OABC by using the formula,
\[=\dfrac{1}{2}\] (sum of parallel sides) \[\times \] height.
So we get, area of shaded region \[=\int\limits_{y=0}^{y=3}{{{y}^{2}}dy}-\] area of OABC.
Don’t confuse the two values of y in the solution. \[y=-1\] will lie in the 4th quadrant as we can observe that there are two intersection points of line and parabola. So just ignore \[y=-1\] and take another value of y.