Question

The area (in sq. units) of the smaller potion enclosed between the curves, ${{x}^{2}}+{{y}^{2}}=4$ and ${{y}^{2}}=3x$, is.
(a) $\dfrac{1}{\sqrt{3}}+\dfrac{4\pi }{3}$
(b) $\dfrac{1}{2\sqrt{3}}+\dfrac{\pi }{3}$
(c) $\dfrac{1}{2\sqrt{3}}+\dfrac{2\pi }{3}$
(d) $\dfrac{1}{\sqrt{3}}+\dfrac{2\pi }{3}$

Answer 1

Hint: To understand the question better, we will first draw the figure of the curves ${{x}^{2}}+{{y}^{2}}=4$ and ${{y}^{2}}=3x$. Then we will solve the equations of the curves to get the coordinates of the points at which they intersect. Then, we find the area under the individual curves. Then we will add these areas.

Complete step by step answer:
The first curve given to us is ${{x}^{2}}+{{y}^{2}}=4$.
As we can see, the curve is a circle with centre at the origin and the radius as 2 units.
The second curve given to us is ${{y}^{2}}=3x$.
This curve is a parabola with the vertex at the origin and focus at (3, 0).
The diagram of the curves are as follows:

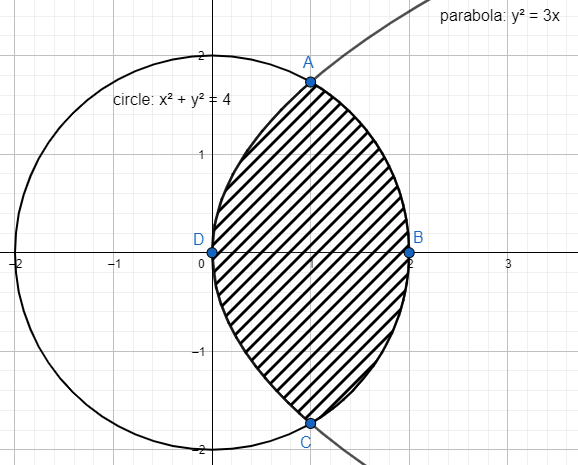
We have to find the area of the curves between ABCD (region with hatching lines).
Coordinates of point D is (0, 0) and that of point B is (2, 0)
As we can see, the area is divided into two parts. If we find the area of one of the parts, we can multiply that area by 2 to get the total area.
To find point A, we have to solve the equation of the circle ${{x}^{2}}+{{y}^{2}}=4$ and the parabola ${{y}^{2}}=3x$.
We will substitute ${{y}^{2}}=3x$ into ${{x}^{2}}+{{y}^{2}}=4$
$\begin{align}
  & \Rightarrow {{x}^{2}}+3x=4 \\
 & \Rightarrow {{x}^{2}}+3x-4=0 \\
\end{align}$
This is a quadratic equation for x. We will solve this quadratic equation by factorisation method.
We will split the middle terms as 4x and ─ x.
$\begin{align}
  & \Rightarrow {{x}^{2}}+4x-x-4=0 \\
 & \Rightarrow x\left( x+4 \right)-1\left( x+4 \right)=0 \\
 & \Rightarrow \left( x+4 \right)\left( x-1 \right)=0 \\
\end{align}$
Thus x = ─ 4 and x = 1. But we can see that ${{y}^{2}}=3x$ doesn’t exist for negative values.
Therefore x – coordinate of point A is 1.
We will integrate the curve $y=\sqrt{3x}$ from 0 to 1 and $y=\sqrt{4-{{x}^{2}}}$ from 1 to 2 and add them up. This will give us the area of the upper part.
\[\begin{align}
  & \Rightarrow \dfrac{1}{2}A=\int\limits_{0}^{1}{\sqrt{3x}}dx+\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}}dx \\
 & \Rightarrow \dfrac{1}{2}A=\sqrt{3}\left( \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right)_{0}^{1}+\left( \dfrac{x}{2}\sqrt{4-{{x}^{2}}}+2{{\sin }^{-1}}\dfrac{x}{2} \right)_{1}^{2} \\
 & \Rightarrow \dfrac{1}{2}A=\sqrt{3}\left( \dfrac{2}{3} \right)+\left\{ 2\dfrac{\pi }{2}-\left( \dfrac{\sqrt{3}}{2}+\dfrac{\pi }{3} \right) \right\} \\
 & \Rightarrow \dfrac{1}{2}A=\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}}{2}+\dfrac{2\pi }{3} \\
 & \Rightarrow \dfrac{1}{2}A=\dfrac{1}{2\sqrt{3}}+\dfrac{2\pi }{3} \\
 & \Rightarrow A=\dfrac{1}{\sqrt{3}}+\dfrac{4\pi }{3} \\
\end{align}\]
So, the correct answer is “Option A”.

Note: It is always advised to draw figures whenever possible. It might give insights to the question and reveal information, which might be overseen without the figures.