Question

The area (in sq. units) of the region described by \[\{\left( x,y \right):{{y}^{2}}\le 2x,y\ge 4x-1\}\] is:
(a) $\dfrac{7}{32}$
(b) $\dfrac{5}{64}$
(c) $\dfrac{15}{64}$
(d) $\dfrac{9}{32}$

Answer 1

Hint: Start by drawing the diagram of the situation given in the question. If you observe, you will see that the inequality ${{y}^{2}}\le 2x$ represents the region inside the parabola ${{y}^{2}}=2x$ and the inequality \[y\ge 4x-1\] represents the area on one side of the line $y=4x-1$ . So, to find the area use the method of definite integration. For limits of integration, find the x-coordinate of intersection of the boundaries of two regions represented by the inequalities given in the question. To make the question easier, just find the area of the region enclosed above the x-axis and double it to get the total area.

Complete step-by-step answer:
We know that the equation ${{y}^{2}}=2x$ represents a parabola with vertex at origin. So, the inequality ${{y}^{2}}\le 2x$ represents the region inside the parabola ${{y}^{2}}=2x$ . Also, the equation $y=4x-1$ represents a straight line.
Let us draw the representative figure of the situation given the question.

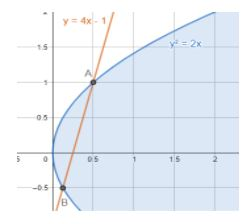
So, according to the question, we need to find the area of the region AOB, where O is the origin.
First, let us find the x-coordinates of the point A and B, which is the intersection of the curves ${{y}^{2}}=2x$ and $y=4x-1$ . so, let us substitute y from equation of line in the equation of parabola, on doing so, we get
${{y}^{2}}=2x$
$\Rightarrow {{\left( 4x-1 \right)}^{2}}=2x$
\[\Rightarrow 16{{x}^{2}}+1-8x-2x=0\]
\[\Rightarrow 16{{x}^{2}}-10x+1=0\]
As the above equation is a quadratic equation, we will use the quadratic formula.
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}=\dfrac{10\pm \sqrt{100-64}}{2\times 16}=\dfrac{10\pm 6}{32}$
So, the possible values of x are $\dfrac{10+6}{32}=\dfrac{1}{2}\text{ and }\dfrac{10-6}{32}=\dfrac{1}{8}$ .
So, the x-coordinate of A is $\dfrac{1}{2}$ and that of B is $\dfrac{1}{8}$ . The y-coordinates corresponding to them are 1 and $\dfrac{-1}{2}$ which we get by putting x-coordinates in the equation of line. So, A = $\left( \dfrac{1}{2},1 \right)$ and B = $\left( \dfrac{1}{8},-\dfrac{1}{2} \right)$ .
Now, let us draw a diagram which focuses on the part which we are dealing with.

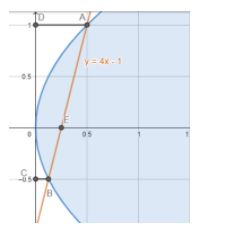
So, ABCD is a trapezium and if we subtract the area of the parabola enclosed with the y axis in the region ABCD, we get the required area.
So, the area of trapezium ABCD = $\dfrac{1}{2}\times \left( \text{sum of }\!\!|\!\!\text{ }\!\!|\!\!\text{ sides} \right)\times \left( \text{distance between parallel sides} \right)$
The length of the parallel sides CB and AD is the x-coordinates of A and B, as they are parallel to x-axis and the distance between them is the difference of the y-coordinates of A and B.
Area of trapezium ABCD = $\dfrac{1}{2}\times \left( \dfrac{1}{8}+\dfrac{1}{2} \right)\times \left( 1-\left( \dfrac{-1}{2} \right) \right)=\dfrac{1}{2}\times \dfrac{5}{8}\times \dfrac{3}{2}=\dfrac{15}{32}$
Now, let us find the area bounded by the parabola with the y-axis, in the region of ABCD. Area bounded by any general curve y=f(x), in region y=a to y=b is given by $\int\limits_{a}^{b}{xdy}$ .
$\text{Area bounded by parabola in ABCD}=\int\limits_{-\dfrac{1}{2}}^{1}{xdy}\text{ }$
Equation of parabola is: ${{y}^{2}}=2x\Rightarrow x=\dfrac{{{y}^{2}}}{2}$ . If we substitute the value of x in the integral, we get
$\text{Area bounded by parabola in ABCD}=\int\limits_{-\dfrac{1}{2}}^{1}{\dfrac{{{y}^{2}}}{2}dy}\text{ }$
Now, we know that $\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}+c}$ . So, we get
$\text{Area bounded by parabola in ABCD}=\left. \dfrac{{{y}^{3}}}{3\times 2} \right|_{-\dfrac{1}{2}}^{1}\text{=}\dfrac{1}{6}+\dfrac{1}{6\times {{2}^{3}}}\text{=}\dfrac{1}{6}+\dfrac{1}{48}\text{=}\dfrac{9}{48}\text{ }$
So, the area of required region is:
$\text{Area of ABCD}-\text{Area bounded by parabola in ABCD}$
$\text{=}\dfrac{15}{32}-\dfrac{9}{48}=\dfrac{1}{16}\left( \dfrac{15}{2}-\dfrac{9}{3} \right)=\dfrac{1}{16}\left( \dfrac{15}{2}-3 \right)=\dfrac{1}{16}\times \dfrac{9}{2}=\dfrac{9}{32}\text{ sq}\text{. units}$

So, the correct answer is “Option (d)”.

Note: Learn the graphs of different standard functions, as in such questions, the most important part is the diagram and for drawing the diagram you need to know the curves. Also, be familiar with approximate values of roots of single digit numbers, as they are used very often. Also, be careful about the calculation part, as the calculation part is very complex and approximation is required to reach an approximate value.