Question

The area (in sq. units) bounded by the parabola $y={{x}^{2}}-1$, the tangent at the point (2,3) to it and the y-axis is
$\begin{align}
  & \left( A \right)\dfrac{14}{3} \\
 & \left( B \right)\dfrac{56}{3} \\
 & \left( C \right)\dfrac{8}{3} \\
 & \left( D \right)\dfrac{32}{3} \\
\end{align}$

Answer 1

Hint: We start solving this question by finding the slope of the tangent to the curve at (2,3) by differentiating the curve and substituting the point (2,3) and we use the formula $\dfrac{d}{dx}{{x}^{n}}=n\times {{x}^{n-1}}$. From the obtained slope and point we find the equation of line using the formula, $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$. Then we plot the graph of the curve and the tangent. Then we divide the region into two parts and find their areas by integrating them using the formula $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}$ and add them to find the total area.

Complete step-by-step solution:
Given that a tangent is drawn to the parabola $y={{x}^{2}}-1$ at point (2,3). So, let us find the equation of the tangent to the curve.
To find the slope of the tangent, let us differentiate the equation with respective to x.
$\begin{align}
  & \dfrac{dy}{dx}=\dfrac{d}{dx}\left( {{x}^{2}}-1 \right) \\
 & \dfrac{dy}{dx}=2x \\
\end{align}$
Then at point (2,3), slope of tangent is,
$\dfrac{dy}{dx}={{\left. 2x \right]}_{x=2}}=4$
So, slope of the tangent is equal to 4.
Now let us consider the formula for line equation from slope and point.
$\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$
So, using the above formula we get,

$\begin{align}
  & \Rightarrow \left( y-3 \right)=4\left( x-2 \right) \\
 & \Rightarrow y-3=4x-8 \\
 & \Rightarrow y=4x-5 \\
\end{align}$
So, equation of the tangent at (2,3) is $y=4x-5$.
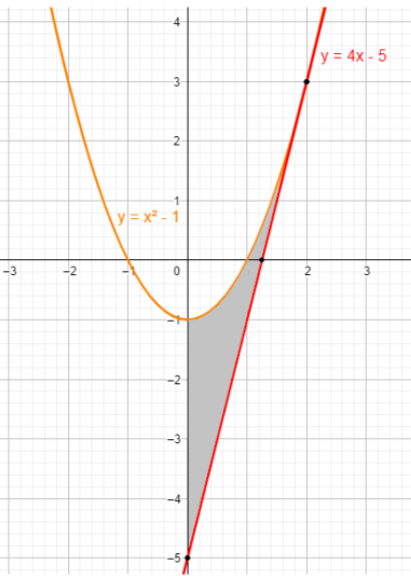
Now, let us plot the graph for the given curves.

Now, let us divide our required region into two parts, above x-axis and below x-axis. So, let us find the point where the line intersects x-axis. On x-axis y=0. So,
$\begin{align}
  & \Rightarrow 4x-5=0 \\
 & \Rightarrow 4x=5 \\
 & \Rightarrow x=\dfrac{5}{4} \\
\end{align}$
Let us use the formula for finding the area between two curves $f\left( x \right)$ and $g\left( x \right)$ and x-axis between x=a and x=b is
 $\int\limits_{a}^{b}{\left( f\left( x \right)-g\left( x \right) \right)dx}$
Using the above formula, for the region below x-axis, we get
$\begin{align}
  & \Rightarrow \int\limits_{0}^{\dfrac{5}{4}}{\left( \left( 4x-5 \right)-\left( {{x}^{2}}-1 \right) \right)dx} \\
 & \Rightarrow \int\limits_{0}^{\dfrac{5}{4}}{\left( -{{x}^{2}}+4x-4 \right)dx} \\
 & \Rightarrow \left[ -\dfrac{{{x}^{3}}}{3}+2{{x}^{2}}-4x \right]_{0}^{\dfrac{5}{4}} \\
 & \Rightarrow \left[ \left( -\dfrac{{{\left( \dfrac{5}{4} \right)}^{3}}}{3}+2{{\left( \dfrac{5}{4} \right)}^{2}}-4\left( \dfrac{5}{4} \right) \right)-\left( -\dfrac{{{0}^{3}}}{3}+2{{\left( 0 \right)}^{2}}-4\left( 0 \right) \right) \right] \\
 & \Rightarrow \left[ \left( -\dfrac{\dfrac{125}{64}}{3}+2\left( \dfrac{25}{16} \right)-5 \right)-\left( 0 \right) \right] \\
 & \Rightarrow \left( -\dfrac{125}{192}+\dfrac{25}{8}-5 \right) \\
 & \Rightarrow \left( \dfrac{475}{192}-5 \right) \\
 & \Rightarrow \left( \dfrac{475}{192}-5 \right) \\
 & \Rightarrow -\dfrac{485}{192} \\
\end{align}$
As the area is positive quantity, we take the area of first part as $\dfrac{485}{192}$…………(1)
Now, let us find the area of second part that is above x-axis.
$\begin{align}
  & \Rightarrow \int\limits_{\dfrac{5}{4}}^{2}{\left( \left( {{x}^{2}}-1 \right)-\left( 4x-5 \right) \right)dx} \\
 & \Rightarrow \int\limits_{\dfrac{5}{4}}^{2}{\left( {{x}^{2}}-4x+4 \right)dx} \\
 & \Rightarrow \left[ \dfrac{{{x}^{3}}}{3}-2{{x}^{2}}+4x \right]_{\dfrac{5}{4}}^{2} \\
 & \Rightarrow \left[ \left( \dfrac{{{2}^{3}}}{3}-2{{\left( 2 \right)}^{2}}+4\left( 2 \right) \right)-\left( \dfrac{{{\left( \dfrac{5}{4} \right)}^{3}}}{3}-2{{\left( \dfrac{5}{4} \right)}^{2}}+4\left( \dfrac{5}{4} \right) \right) \right] \\
 & \Rightarrow \left[ \left( \dfrac{8}{3}-8+8 \right)-\left( \dfrac{\dfrac{125}{64}}{3}-2\left( \dfrac{25}{16} \right)+5 \right) \right] \\
 & \Rightarrow \left( \dfrac{8}{3} \right)-\left( \dfrac{125}{192}-\dfrac{25}{8}+5 \right) \\
 & \Rightarrow \left( \dfrac{8}{3} \right)-\left( -\dfrac{475}{192}+5 \right) \\
 & \Rightarrow \dfrac{8}{3}-\dfrac{485}{192} \\
 & \Rightarrow \dfrac{27}{192}.................\left( 2 \right) \\
\end{align}$
Then the total area is sum of both areas. So, adding the obtained areas in equation (1) and (2) we get,
$\begin{align}
  & \Rightarrow \dfrac{485}{192}+\dfrac{27}{192} \\
 & \Rightarrow \dfrac{512}{192} \\
 & \Rightarrow \dfrac{8}{3} \\
\end{align}$
So, total area of the region bounded by given curves is $\dfrac{8}{3}$ square units.
Hence answer is Option C.

Note: There is a possibility of making a mistake while solving this question by not taking the modulus of $-\dfrac{485}{192}$, and leaving it as it is. Then they add it with $\dfrac{27}{192}$ to find the total area. But it is wrong. The first part of the region is below the x-axis that is the reason we get the area as negative. So, we need to take the modulus of the area of the first part $-\dfrac{485}{192}$, and add it to $\dfrac{27}{192}$.