Question

The area enclosed the between the parabola \[{\text{y = }}{{\text{x}}^{\text{2}}}{\text{ - x + 2}}\]and the line\[{\text{y = x + 2}}\] in sq equal to
A.\[\dfrac{{\text{8}}}{{\text{3}}}\]
B.\[\dfrac{{\text{1}}}{{\text{3}}}\]
C.\[\dfrac{{\text{2}}}{{\text{3}}}\]
D.\[\dfrac{{\text{4}}}{{\text{3}}}\]

Answer 1

Hint: draw the diagram and find the point of intersection of the given curve so we can get the varying limit of x and then apply the formula
Of \[\int {\left( {{\text{uppercurve - lowercurve}}} \right){\text{dx}}} \]. Thus apply the limit in the formula of integration and proceed with the rules of integration and calculate the required area.

Complete step by step solution:
Diagram :

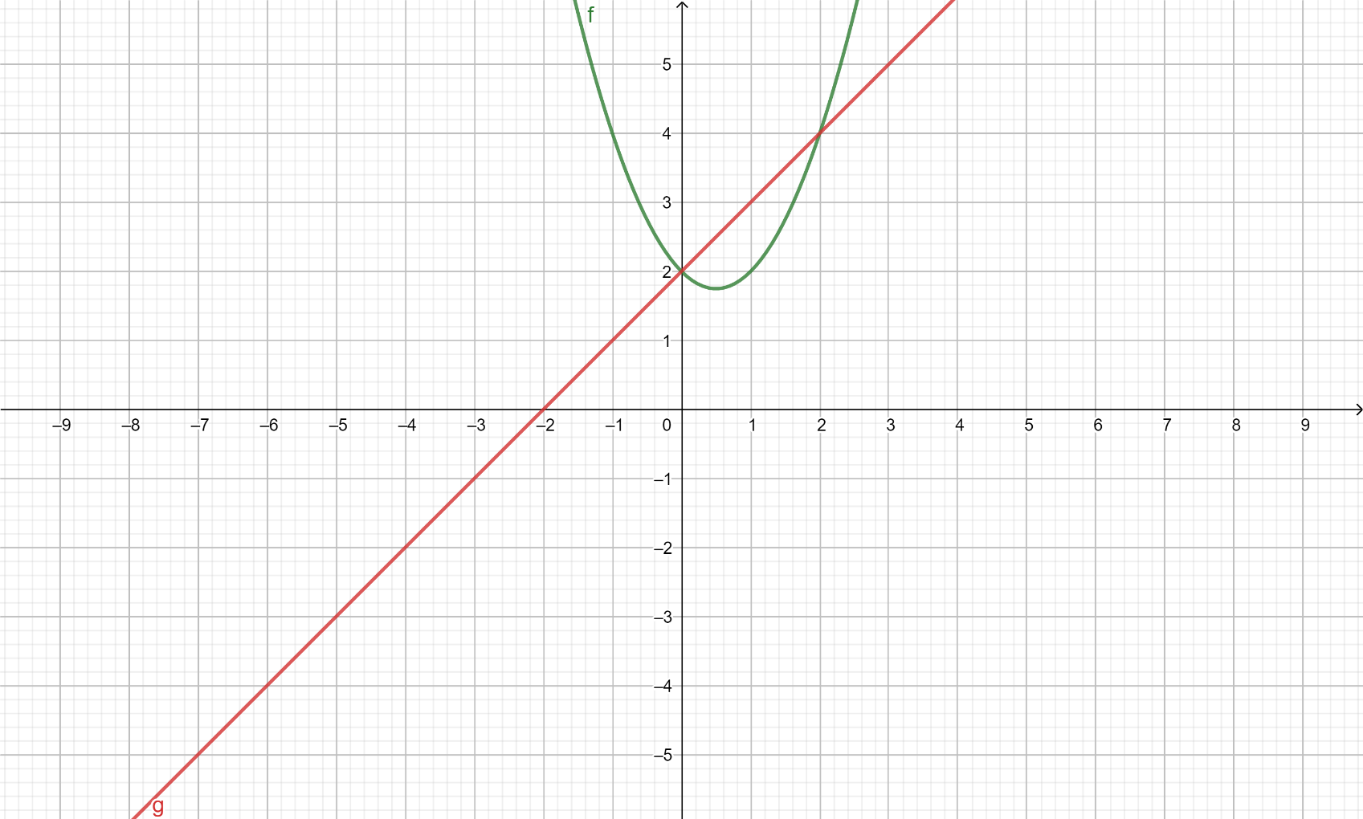
Equate both the equations to find their point of intersection as it will be our limit as from start point to end point.
\[{{\text{x}}^{\text{2}}}{\text{ - x + 2 = x + 2}}\]
\[{{\text{x}}^{\text{2}}}{\text{ - 2x = 0}}\]
\[{\text{x}}\left( {{\text{x - 2}}} \right){\text{ = 0}}\]
\[{\text{x = 0,2}}\]
On making diagram we can observe that
A=\[\int {\left( {{\text{upper curve - lower curve}}} \right){\text{dx}}} \]
=\[\int {{\text{x + 2 - (}}{{\text{x}}^{\text{2}}}{\text{ - x + 2)}}{\text{.dx}}} \]
=\[\int_{\text{0}}^{\text{2}} {{\text{2x - }}} {{\text{x}}^{\text{2}}}{\text{.dx}}\]
${\text{ = }}\dfrac{{{\text{2}}{{\text{x}}^{\text{2}}}}}{{\text{2}}}\left| {{{\text{0}}^{\text{2}}}{\text{ - }}\dfrac{{{{\text{x}}^{\text{3}}}}}{{\text{3}}}} \right|_{\text{0}}^{\text{2}}$
$\dfrac{{{\text{2}}\left( {{{\text{2}}^{\text{2}}}} \right)}}{{\text{2}}}{\text{ - }}\dfrac{{{{\text{2}}^{\text{3}}}}}{{\text{3}}}$
\[{\text{ = 4 - }}\dfrac{{\text{8}}}{{\text{3}}}\]
\[{\text{ = }}\dfrac{{\text{4}}}{{\text{3}}}\]sq. unit
Hence option D is correct answer
Note: To Find the area Enclosed between 2 given curves always first always find the points of intersection of the curves and then use definite integral between the two points. To calculate the area always subtract the lower curve from the upper curve, for the curve y=f(x) between x=a and x=b, one must integrate y=f(x) between the limits of a and b.