Question

The area enclosed by the curve \[y={{\sin }^{3}}x\], x-axis between \[x=0\] to \[x=\dfrac{\pi }{2}\] is:
A. \[1\]
B. \[{}^{1}/{}_{3}\]
C. \[{}^{2}/{}_{3}\]
D. \[{}^{3}/{}_{2}\]

Answer 1

Hint: Relate the graph of \[\sin x\] and \[{{\sin }^{3}}x\] by the range of \[\sin x\], i.e. [-1, 1]. Draw a neat diagram to get the area of the bounded part from the given curves. Area bounded by lines, x = a, x = b, and y = f(x) will be \[=\int\limits_{a}^{b}{f(x)dx}\] where (b > a).

Complete step by step answer:
Here, we need to determine the area bounded by \[y={{\sin }^{3}}x\], x-axis and between x = 0 and \[x=\dfrac{\pi }{2}\]. So first of all we need to represent the area in the diagram by drawing graph of \[y={{\sin }^{3}}x\], \[x=0\], \[x=\dfrac{\pi }{2}\].
So we can draw the diagram as:-

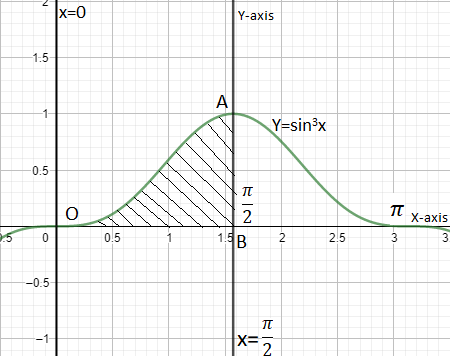
Now we can observe from the above diagram and get that the area of the shaded region is the required area of the problem. Here, the graph of \[{{\sin }^{3}}x\] will be just like sinx, as the range of sinx is [-1, 1].
Hence, the range of \[{{\sin }^{3}}x\] will be [-1, 1] as well. So we can get the area of the shaded region by integrating \[y={{\sin }^{3}}x\] from x = 0 to \[\dfrac{\pi }{2}\].
Hence, area can be calculated as,
Area of the shaded region \[=\int\limits_{0}^{{}^{\pi }/{}_{2}}{{{\sin }^{3}}xdx}....(1)\]
Now we know the identity of sin3x is given as,
\[\sin 3x=3\sin x-4{{\sin }^{3}}x.....(2)\]
So we can calculate the value of \[{{\sin }^{3}}x\] from the above equation and hence put it to the equation (1) to get a simple form of integral.
Hence, value of \[{{\sin }^{3}}x\] can be given as,
\[\begin{align}
  & sin3x=3 sinx-4{{\sin }^{3}}x \\
 & 4{{\sin }^{3}}x=3\sin x-\sin 3x \\
 & {{\sin }^{3}}x=\dfrac{3\sin x-\sin 3x}{4}......(3) \\
\end{align}\]
Hence putting value of \[{{\sin }^{3}}x\] to the equation (1), we get,
Area of shaded region \[=\int\limits_{0}^{{}^{\pi }/{}_{2}}{\dfrac{3\sin x-\sin 3x}{4}}dx\]
\[\begin{align}
  & =\dfrac{1}{4}\int\limits_{0}^{{}^{\pi }/{}_{2}}{\left( 3\sin x-\sin 3x \right)dx} \\
 & =\dfrac{1}{4}\left( 3\int\limits_{0}^{{}^{\pi }/{}_{2}}{\sin xdx-}\int\limits_{0}^{{}^{\pi }/{}_{2}}{\sin 3x}dx \right) \\
\end{align}\]
As we know, \[\int{\sin x dx=-\cos x}\], we get,
Area of the shaded region,
\[\begin{align}
  & =\dfrac{1}{4}\left( 3\left( -\operatorname{cosx} \right)_{0}^{{}^{\pi }/{}_{2}}-\left( \dfrac{-\cos 3x}{3} \right)_{0}^{{}^{\pi }/{}_{2}} \right) \\
 & =\dfrac{1}{4}\left( 3\left( -\cos \dfrac{\pi }{2}+\cos 0 \right)-\left( \dfrac{-\cos \dfrac{3\pi }{2}}{3}+\dfrac{\cos 0}{3} \right) \right) \\
 & =\dfrac{1}{4}\left( 3-\dfrac{1}{3} \right)=\dfrac{8}{3}\times \dfrac{1}{4}=\dfrac{2}{3}uni{{t}^{2}} \\
\end{align}\]
Hence the area of the bounded area is \[\dfrac{2}{3}uni{{t}^{2}}\].
So option C is the correct answer.
Note:
Curve \[xy=1\] is a rectangular hyperbola because the expression \[xy=1\] or \[x=\dfrac{1}{y}\] has an inverse relation in x and y. So if x increases, then y will decrease and vice-versa. That’s why the curves in all 4 quadrants have an inverse relation. One may easily understand the curve of \[xy=1\] by this approach.
Diagrams play an important role for this type of question.
Another approach for getting area of bounded region from the diagram would be given as,
Area of shaded region = area of triangle OTC – area of TAB
where, we need to calculate area of TAB by difference of area of DATC and area of DABC. So it can be another approach.