Question

The area bounded by \[{{x}^{2}}=4ay\] and $y=2a$ is?
A. $\dfrac{16\sqrt{2}{{a}^{2}}}{3}$
B. $\dfrac{16{{a}^{2}}}{3}$
C. $\dfrac{8{{a}^{2}}}{3}$
D. $\dfrac{8\sqrt{2}{{a}^{2}}}{3}$

Answer 1

Hint: We have been given two functions and we have to find the area that is bounded by them. For this, we will first find the points of intersections of these functions. Then using those, we will plot the graph of both those functions combined. As a result, we will be able to see the required area. Then we will use definite integration to find this area. For that, we will use the formula written as follows:
The area bounded by two graphs ${{y}_{1}}=f\left( x \right)$ and ${{y}_{2}}=g\left( x \right)$ where the points of intersection of these graphs are $\left( {{a}_{1}},{{b}_{1}} \right)$ and $\left( {{a}_{2}},{{b}_{2}} \right)$ where ${{a}_{2}}>{{a}_{1}}$ and g(x) lies above f(x) on the graph, is given as:
$Area=\int_{{{a}_{1}}}^{{{a}_{2}}}{\left( {{y}_{2}}-{{y}_{1}} \right)dx}$
Then we will put in the required values given in the question and solve it accordingly by the formula $\int_{a}^{b}{{{x}^{n}}dx}=\left[ \dfrac{{{x}^{n+1}}}{n+1} \right]_{a}^{b}$. Thus, we will get our required answer.

Complete step by step answer:
We have been given two curves \[{{x}^{2}}=4ay\] and $y=2a$ and we have to find the area bounded by these two curves.
To find that, we will first find the points of intersection of the two curves. This is done as follows:
Now, we have the following two equations:
\[{{x}^{2}}=4ay\] …..(i)
$y=2a$ …..(ii)
Now, putting the value of y from equation (ii) in equation (i), we get:
$\begin{align}
  & {{x}^{2}}=4ay \\
 & \Rightarrow {{x}^{2}}=4a\left( 2a \right) \\
 & \Rightarrow {{x}^{2}}=8{{a}^{2}} \\
\end{align}$
Now, taking square root both sides, we get the values of x as:
$\begin{align}
  & {{x}^{2}}=8{{a}^{2}} \\
 & \Rightarrow x=\pm 2\sqrt{2}a \\
\end{align}$
Thus, the points of intersection of the two curves are $\left( 2\sqrt{2}a,2a \right)$ and $\left( -2\sqrt{2}a,2a \right)$.
Now that we have the points of intersections of these curves, we will draw their curve.
The first curve is a parabola given as ${{x}^{2}}=4ay$
Now, we can see that this parabola is an upward parabola with (0,0) as its vertices and (0,a) as its focus.
The second curve is a line given as $y=2a$ which is a line parallel to x-axis.
Thus, the graph of these two curves become:

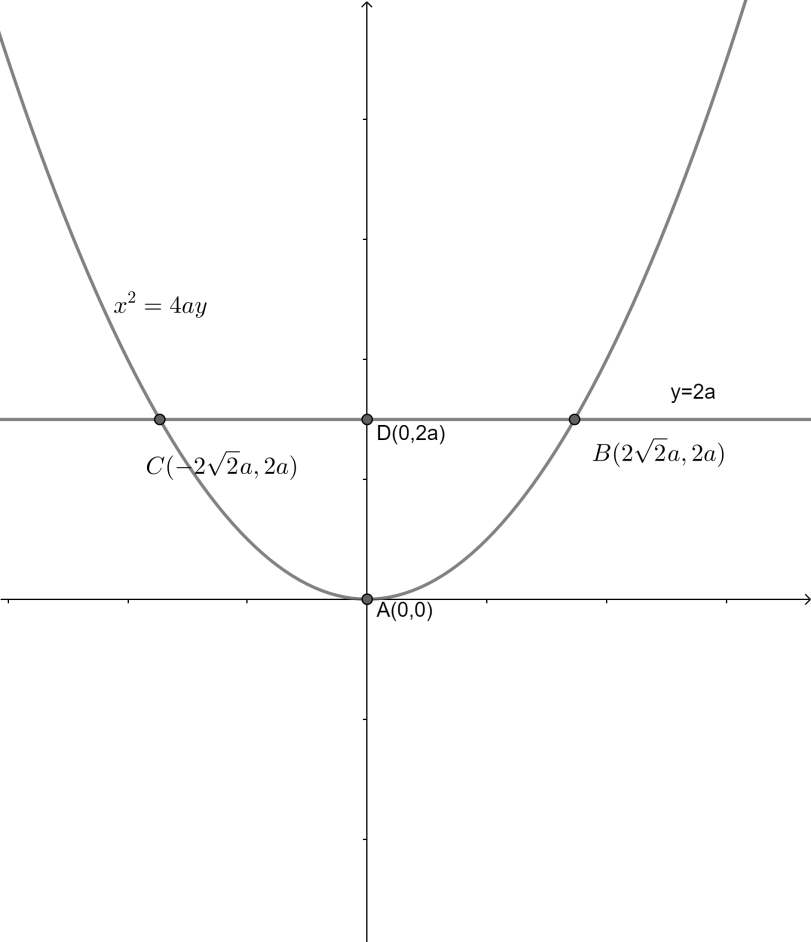
Now, from the figure we can see that the area bounded by the points ABDCA is the required area.
Now, we will find the required area by the process of definite integration.
We know that area bounded by two graphs ${{y}_{1}}=f\left( x \right)$ and ${{y}_{2}}=g\left( x \right)$ where the points of intersection of these graphs are $\left( {{a}_{1}},{{b}_{1}} \right)$ and $\left( {{a}_{2}},{{b}_{2}} \right)$ where ${{a}_{2}}>{{a}_{1}}$ and g(x) lies above f(x) on the graph, is given as:
$Area=\int_{{{a}_{1}}}^{{{a}_{2}}}{\left( {{y}_{2}}-{{y}_{1}} \right)dx}$
Here, we can see from the graph that:
$\begin{align}
  & g\left( x \right):y=2a \\
 & f\left( x \right):{{x}^{2}}=4ay\Rightarrow y=\dfrac{{{x}^{2}}}{4a} \\
\end{align}$
Thus, we have:
$\begin{align}
  & {{y}_{1}}=2a \\
 & {{y}_{2}}=\dfrac{{{x}^{2}}}{4a} \\
 & {{a}_{1}}=0 \\
 & {{a}_{2}}=2\sqrt{2}a \\
\end{align}$
Now, here we can see that the area under bounded by ABDA and ACDA are equal. Hence, the required area will be twice the area of any one of these parts.
Thus, taking the ABDA part, we get the required area as:
$\begin{align}
  & Area=2\int_{{{a}_{1}}}^{{{a}_{2}}}{\left( {{y}_{2}}-{{y}_{1}} \right)dx} \\
 & \Rightarrow Area=2\int_{0}^{2\sqrt{2}a}{\left( 2a-\dfrac{{{x}^{2}}}{4a} \right)dx} \\
\end{align}$
Now, we will solve this integral.
We know that $\int_{a}^{b}{{{x}^{n}}dx}=\left[ \dfrac{{{x}^{n+1}}}{n+1} \right]_{a}^{b}$
Thus, applying this in our integral, we get:
$\begin{align}
  & Area=2\int_{0}^{2\sqrt{2}a}{\left( 2a-\dfrac{{{x}^{2}}}{4a} \right)dx} \\
 & \Rightarrow Area=2\left[ 2ax-\dfrac{{{x}^{3}}}{12a} \right]_{0}^{2\sqrt{2}a} \\
 & \Rightarrow Area=2\left[ \left( 2a\left( 2\sqrt{2}a \right)-\dfrac{{{\left( 2\sqrt{2}a \right)}^{3}}}{12a} \right)-\left( 2a\left( 0 \right)-\dfrac{{{\left( 0 \right)}^{3}}}{12a} \right) \right] \\
\end{align}$
Now, solving this, we get:
$\begin{align}
  & Area=2\left[ \left( 2a\left( 2\sqrt{2}a \right)-\dfrac{{{\left( 2\sqrt{2}a \right)}^{3}}}{12a} \right)-\left( 2a\left( 0 \right)-\dfrac{{{\left( 0 \right)}^{3}}}{12a} \right) \right] \\
 & \Rightarrow Area=2\left[ \left( 4\sqrt{2}{{a}^{2}}-\dfrac{16\sqrt{2}{{a}^{3}}}{12a} \right)-\left( 0-\dfrac{0}{12a} \right) \right] \\
 & \Rightarrow Area=2\left[ 4\sqrt{2}{{a}^{2}}-\dfrac{4\sqrt{2}{{a}^{2}}}{3} \right] \\
 & \Rightarrow Area=2\left[ \dfrac{12\sqrt{2}{{a}^{2}}-4\sqrt{2}{{a}^{2}}}{3} \right] \\
 & \Rightarrow Area=2\left[ \dfrac{8\sqrt{2}{{a}^{2}}}{3} \right] \\
 & \therefore Area=\dfrac{16\sqrt{2}{{a}^{2}}}{3} \\
\end{align}$
Thus, the required area is $\dfrac{16\sqrt{2}{{a}^{2}}}{3}$ square units.

So, the correct answer is “Option A”.

Note: Here we have doubled the area of the part ABDA to find the required area instead of using the direct formula to find the area of ABCA. We could have directly used that too but as both these functions are odd functions and the values of both the limits are same but equal in sign, i.e. are in the form of -a to a, the function would have came out the same as follows:
$Area=\int_{-2\sqrt{2}a}^{2\sqrt{2}a}{\left( 2a-\dfrac{{{x}^{2}}}{4a} \right)dx}$
Now we know that if $f\left( -x \right)=f\left( x \right)$ , then $\int_{-a}^{a}{f\left( x \right)dx}=2\int_{0}^{a}{f\left( x \right)dx}$.
Now, if we take $f\left( x \right)=2a-\dfrac{{{x}^{2}}}{4a}$ , then $f\left( -x \right)$ will come out as:
$\begin{align}
  & f\left( -x \right)=2a-\dfrac{{{\left( -x \right)}^{2}}}{4a} \\
 & \Rightarrow f\left( -x \right)=2a-\dfrac{{{x}^{2}}}{4a} \\
 & \Rightarrow f\left( -x \right)=f\left( x \right) \\
\end{align}$
Thus, we will get the area as:
$\begin{align}
  & Area=\int_{-2\sqrt{2}a}^{2\sqrt{2}a}{\left( 2a-\dfrac{{{x}^{2}}}{4a} \right)dx} \\
 & \Rightarrow Area=2\int_{0}^{2\sqrt{2}a}{\left( 2a-\dfrac{{{x}^{2}}}{4a} \right)dx} \\
\end{align}$