Question

The area bounded by the parabola \[y=4-{{x}^{2}}\] and x-axis in sq. units is:
(a) \[\dfrac{32}{3}\]
(b) \[\dfrac{16}{3}\]
(c) \[\dfrac{8}{3}\]
(d) \[\dfrac{1}{3}\]

Answer 1

Hint: First of all, draw the curve in x – y plane to visualize the question. Now, find the points at which it is the intersection at x-axis by substituting y = 0 in the curve. Suppose the points are a and b. So, find the required area by evaluating the integral \[\int\limits_{a}^{b}{ydx}\]. Here, substitute the value of y as \[\left( 4-{{x}^{2}} \right)\] and use \[\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}\].

Complete step-by-step answer:
In this question, we have to find the area bounded by the parabola \[y=4-{{x}^{2}}\] and x-axis in square units. Let us first see the area bounded by any curve y = f (x) and the x-axis. So, we get the area bounded by the curve y = f (x), the axis and the ordinates x = a and x = b is given by
\[A=\int\limits_{a}^{b}{f\left( x \right)}dx=\int\limits_{a}^{b}{ydx}\]

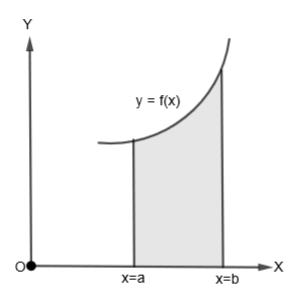
Let us now consider our question. Let us draw the curve \[y=4-{{x}^{2}}\] in the x – y plane.

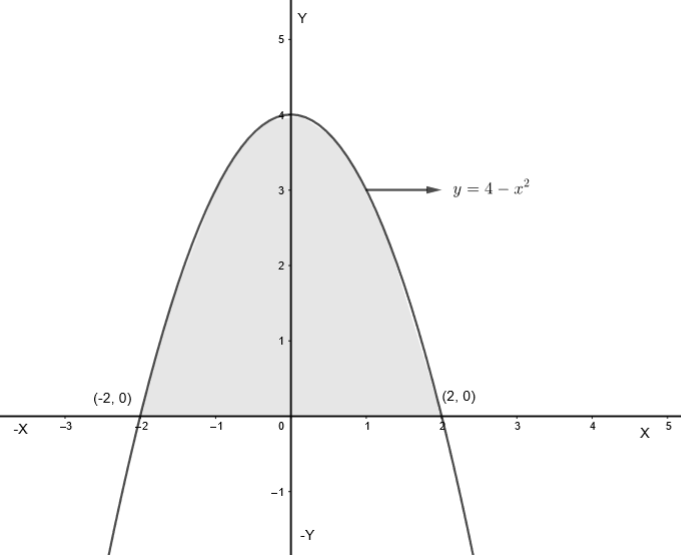
By substituting y = 0, we get,
\[0=4-{{x}^{2}}\]
\[{{x}^{2}}=4\]
\[x=\pm \sqrt{4}\]
\[x=\pm 2\]
So, the curve cuts the x-axis at (2, 0) and (– 2, 0).
So, we get the area enclosed between the curve x-axis and ordinates x = – 2 and x = 2, we get,
\[A=\int\limits_{a}^{b}{f\left( x \right)dx}\]
\[A=\int\limits_{-2}^{2}{\left( 4-{{x}^{2}} \right)dx}\]
We know that,
\[\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}+c\]
So, we get,
\[A=\int\limits_{-2}^{2}{\left( 4{{x}^{0}}-{{x}^{2}} \right)dx}\]
\[A=\int\limits_{-2}^{2}{\left( \dfrac{4{{x}^{0+1}}}{0+1} \right)-\left( \dfrac{{{x}^{2+1}}}{2+1} \right)}\]
\[A=\int\limits_{-2}^{2}{\left( 4x-\dfrac{{{x}^{3}}}{3} \right)}\]
By substituting the limits in the above expression, we get,
\[A=\left[ \left( 4\left( 2 \right)-\dfrac{{{\left( 2 \right)}^{3}}}{3} \right)-\left( 4\left( -2 \right)-\dfrac{{{\left( -2 \right)}^{3}}}{3} \right) \right]\]
\[A=\left[ \left( 8-\dfrac{8}{3} \right)-\left( -8+\dfrac{8}{3} \right) \right]\]
\[A=\left[ \left( \dfrac{16}{3} \right)-\left( \dfrac{-16}{3} \right) \right]\]
\[A=\dfrac{32}{3}sq.units\]
So, option (a) is the right answer.

Note: In this question, many students make this mistake of finding the area between x = 0 and x = 2 but forget to double it and get the wrong answer as (b). So, they must take care that we need to find the area between the ordinates x = – 2 and x = 2. Also, students must note that whenever we find the area under the curve, we always have to take the modulus of it in case it is negative because the area can never be a negative value.